Duas barras, e , suportam uma carga vertical . As barras são feitas do mesmo material e o comprimento, , da horizontal é constante. Entretanto, o ângulo pode variar pelo movimento vertical do ponto , alterando-se o comprimento de para corresponder ás novas posições, Supondo que as tensões admissíveis, à tração e à compressão, sejam iguais e que as barras sejam carregadas até esse valor, determinar o ângulo que dê à estrutura o peso minimo.
Passo 1
Bom galera, vamos começar fazendo um pequeno diagraminha de corpo livre do ponto :
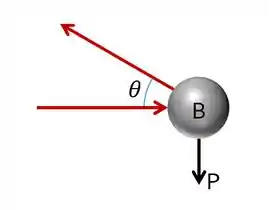
Vamos fazer um equilíbrio de forças:
E também:
Passo 2
Belezinha, agora vamos encontrar algumas informações, vamos lá, primeiro a área das barras:
Enquanto que a largura da barra que varia é dada por:
Passo 3
Show de bolinhas, vamos atrás agora do peso da treliça, onde é a densidade do material.
, , e são constantes e apenas varia com .
Então vamos chamar:
Então ficamos com:
Passo 4
Agora, a gente precisa encontrar o ponto em que o peso é mínimo, vamos então derivar a função que a gente tem e igualar a .
Vamos resolver essa equação agora:
Usamos a propriedade: :