(Adaptada) Dados de testes realizados com uma bomba Peerless de sucção axial do tipo 1430, operando a 1750 rpm, com um rotor de diâmetro 14,0 pol estão na tabela abaixo:

Faça um gráfico representando a curva de operação da bomba e a sua eficiência, se o fluido é a água. Localize no gráfico o ponto de operação de melhor eficiência (BEP ou best efficiency point). Dica: a potência da bomba em hp pode ser calculada através da carga em ft que ela adiciona ao fluido.
Passo 1
E aí, jovem padawan! Esse exercício pede duas coisas: o gráfico da curva de operação e o da eficiência.
Vamos começar pela curva de operação, que é o gráfico da carga da bomba (H) pela vazão (Q). O enunciado já deu uma tabela com esses dois dados. Com isso, vamos apenas plotar cada par (x, y). Nesse caso: (Q, H).
Pontos da curva: (198, 270), (195, 420), (178, 610), (165,720), (123,1000)
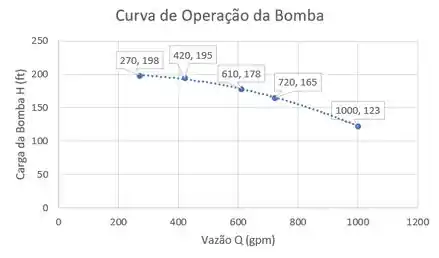
Tcharam! E a primeira parte está respondida!
Passo 2
Agora vamos ao gráfico da eficiência. Como calcular essa variável? Repara que ainda não utilizamos os dados de potência da tabela do enunciado e é por aí mesmo que vamos resolver!
A potência do motor é definida por:
Isolando a eficiência da bomba
Os valores de carga da bomba, vazão volumétrica e potência do motor são dados na tabela. Além disso, é a massa específica da água e g é a gravidade. Ou seja, temos todos esses valores e podemos calcular a eficiência para cada par de pontos (Q, H)
Mas antes, só um detalhe! A carga da bomba foi fornecida em pés, a vazão em galões por minuto e a potência em horse-power. Essas medidas não estão no mesmo sistema. =O Então, vamos passar tudo pro Sistema Internacional (SI) e sermos felizes!
Aplicando os fatores de conversão para o SI:
Sabendo que
Aplicando essa fórmula para cada ponto , temos a eficiência em cada ponto. Vamos fazer mais uma linha na tabela do enunciado:

Para fazer a curva de eficiência da bomba, vamos aproveitar o mesmo gráfico da curva de operação e colocar a eficiência do lado direito na vertical. A curva laranja é de Eficiência versus Vazão Volumétrica:
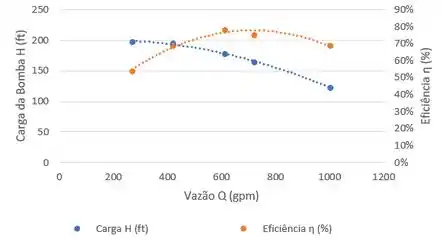
Passo 3
O ponto de operação com maior eficiência conforme calculado na tabela e como pode ser observado no gráfico corresponde a e a eficiência é de 78%

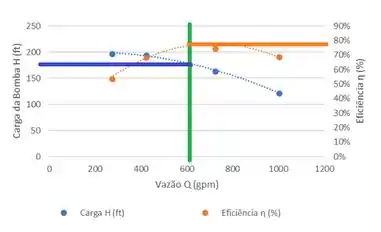
Resposta
Eficiência de 78%