Determinar a distância da reta
- Ao plano
- Ao plano
Passo 1
Temos duas maneiras de resolver esse exercício, vamos resolver a letra “a” da forma mais tradicional (e mais longa) e a letra ”b” de uma forma mais rápida.
Mas vamos começar pela “a”
Lembrando lá da nossa “formulosa” (essa aqui de baixo), precisamos de um ponto da reta e da equação geral do plano.
Um ponto da reta pode ser , mas quem é o meu plano??
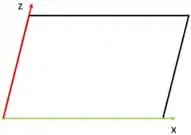
Ahhh, maneiro. Mas qual é a equação dele mesmo??
Vamos descobrir, haha.
Olhando para reta do eixo , tiramos que um vetor diretor é , fazendo o mesmo para o eixo , temos Se a gente fizer vamos achar o vetor normal ao nosso plano !
Achamos , agora vamos substituir na forma geral da equação do plano:
Para descobrir , basta substituir um ponto do plano na equação acima. Um ponto de é , logo
Com isso, a equação geral do plano é
Passo 2
Agora que sabemos , e , podemos substituir na fórmula!
Passo 3
Vamos resolver a letra “b” rapidinho!
O ponto da reta pode ser o mesmo, logo .
Agora, pensa comigo. O plano é o plano formado pelos eixos e , deixando o eixo excluidão. Então, o plano é exatamente o plano .
Com isso, , .
É só colocar na fórmula e partir para o abraço!
E zefini!