O irrigador de gramados horizontal da figura abaixo tem uma vazão d’água de , introduzida verticalmente pelo centro. Calcule o torque resistente necessário para manter os braços sem rotação e a rotação em se não houver torque resistente.
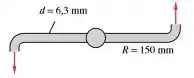
Passo 1
O primeiro passo é estipular o volume de controle, que nesse caso será o próprio irrigador.
Assim a próxima coisa a se fazer é descobrir a velocidade de saída do fluido.
Como sabemos a vazão, descobrir a velocidade não é tão difícil se tivermos a secção reta.
Como temos duas saídas vamos somar a área das duas. Fazendo assim:
A velocidade é:
Observe que passamos a vazão para .
Agora vamos aplicar a equação de momento angular:
Repare que o irrigador gira no sentido anti-horário, o que produz um torque positivo pela regra da mão direita. Como o torque aplicado é um torque resistente (para manter os braços sem rotação), então colocamos o sinal negativo para o torque na equação, para encontrar seu módulo
Lembra do principio da continuidade que falava que em um escoamento incompressível a vazão de entrada é igual a de saída, assim e que se for um escoamento permanente é constante e podemos escrever que
Beleza, então ficamos com:
O que acontece é que nesse problema a velocidade de entrada e o braço de alavanca estão na mesma direção, assim o produto vetorial é nulo. Deixando só:
Só que isso tudo só vale para um referencial inercial, e por isso a velocidade da saída será “ajustada” para um referencial inercial.
Onde esse é a velocidade de entrada da água no irrigador e é a velocidade do irrigador na saída. A velocidade da água na saída é uma relação entre a de entrada (não estamos considerando perdas) e a do irrigador na saída 😉
Agora substituindo na equação que encontramos temos:
A vazão mássica é .
Agora só falta resolvermos o produto vetorial que temos:
Sabemos que é na direção e a velocidade na direção , assim lembrando que é igual a , então temos:
Beleza, agora podemos terminar a equação:
Chegamos na equação que queríamos.
Nesse item queremos o torque para que o irrigador não gire, assim .
Então:
Agora temos que substituir os valores que conhecemos
Passo 2
Agora não há torque, assim temos:
Só falta deixar na unidade certa, uma rotação significa e
Assim: