Considere o mecanismo apresentado na figura, onde o bloco 1 está apoiado em uma superfície sem atrito e o bloco 2 está sustentado por uma polia móvel sem massa (corpo 3 na figura). A polia fixa é ideal. O fio (ideal) conecta o bloco 1 à polia móvel e está fixo ao teto. O fio (ideal) sustenta o bloco 2 à polia 3.
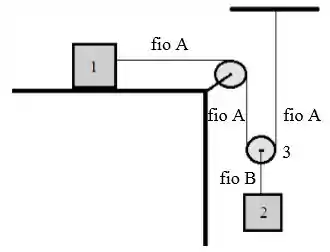
Neste mecanismo, devido ao vínculo existente entre o fio e a polia móvel, o módulo da aceleração do bloco 1, é o dobro do módulo da aceleração do bloco 2, .
As massas dos blocos são e . A massa da polia móvel . Use .
a) Represente os diagramas de corpo livre para os blocos 1 e 2 e para a polia móvel 3, explicitando todas as forças que atuam neles.
b) Escolha sistemas de coordenadas adequados para cada corpo (explicite-os!) e escreva as equações literais (não substitua ainda os valores das massas ou !) resultantes das leis de Newton para os três corpos.
c) A partir das equações do item obtenha literalmente e então substitua os valores fornecidos para encontrar o valor numérico do módulo de .
d) Obtenha o módulo da tração exercida pelo fio sobre o bloco 2.
Passo 1
a)
Basta representar as forças em cada corpo: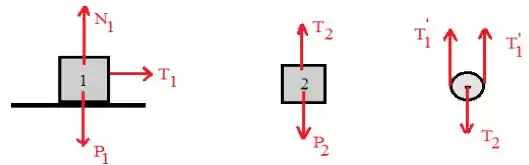
Passo 2
b)
O bloco 1 só tem movimento para a direita, enquanto o bloco 2 e a polia tem movimento vertical para baixo. Assim, pelo acoplamento dos dois movimentos, vamos definir para o bloco 1 o eixo positivo para a esquerda e para o bloco 2 e polia, definimos o eixo positivo para baixo.
Para o corpo 1:
Para o corpo 2:
Para a polia móvel:
Passo 3
c)
Foi dado que (equação de vínculo) (5)
Por outro lado, como as polias são não massivas e o fio 1 inextensível, o módulo de é igual ao módulo de
Usando estas informações, ficamos com as seguintes equações:
Se somamos temos:
Passo 4
d)
Da equação :
Temos:
Daí:
Resposta
a)
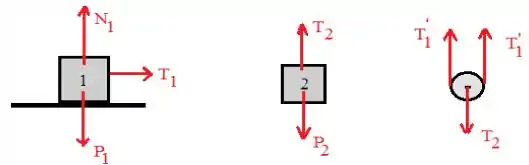
b)
Para o corpo 1:
Para o corpo 2:
Para a polia móvel:
c)
d)