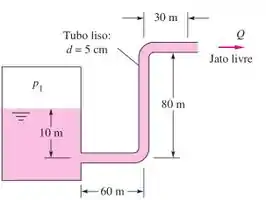
O escoamento no tubo da Figura é produzido pelo ar pressurizado no reservatório. Que pressão manométrica é necessária para fornecer uma vazão de água a 20°C?
Passo 1
Mais uma vez, vamos olhar a equação da energia e descobrir pelo enunciado qual valor de cada propriedade na entrada e na saída.
Queremos descobrir manométrica.
Vamos supor que o reservatório é muito grande, ou seja, não há movimentação na superfície que seja considerável, logo .
Sabemos também que:
Na figura temos que o jato na saída é livre, logo , na escala manométrica.
Se conhecemos o diâmentro do duto e a vazão, podemos calcular a velocidade:
Onde,
Logo nosso é:
Nossa equação fica:
Onde não conhecemos ainda .
Passo 2
Antes de calcularmos , devemos saber se o escoamento é laminar ou não.
Para isso calculamos o número de Reynolds:
Água a tem as seguintes propriedades, e
Temos escoamento não-laminar.
Como o enunciado não informou nada, vamos supor que o tubo seja liso. A partir do Diagrama de Moody:
Substituindo na expressão de ,
Passo 3
Substituindo na expressão de