Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
O exercício pede para vermos se um sistema é estável ou não usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e determinaremos a estabilidade do sistema usando o critério de Nyquist no gráfico gerado pelo MATLAB.
Passo 2
O primeiro passo para resolver o exercício é entrar com no MATLAB. Para isto, usaremos a função , que cria funções de transferência e tem a seguinte sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script, vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente ao de menor expoente:

Logo abaixo, já incluimos o comando para criar , que será armazenado na variável .
Se quiser conferir se você entrou certinho, rode o programa que você tem até agora e peça para o MATLAB imprimir no Command Window. Se estiver tudo certo, você terá:

Passo 3
Tendo entrado com no MATLAB, podemos plotar o diagrama de Nyquist, usando a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :
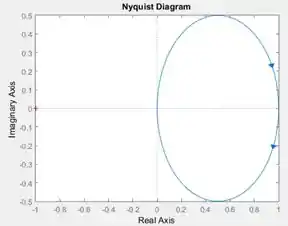
Passo 4
Com o diagrama de Nyquist em mãos, podemos avaliar a estabilidade do sistema usando o critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de ;
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Neste exercício, o denominador de é , que tem como raiz . Logo, o único polo de é e ele é negativo. Portanto, não tem polos positivos e .
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo anterior:

Tem uma cruzinha vermelha na extremidade esquerda do gráfico, reparou? Essa cruzinha marca o ponto de coordenadadas . Como a cruzinha está fora do diagrama de Nyquist (que é o círculo azul com flechinhas), o diagrama não dá volta alguma em torno de , logo,
Tendo e , calculamos . Temos que . Como , o sistema é estável.
Resposta
Sistema estável