Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:
Passo 1
O exercício pede para vermos se um sistema é estável ou não usando o critério de Nyquist. Para isto, usaremos a função do MATLAB para plotar o diagrama de Nyquist de e determinaremos a estabilidade do sistema usando o critério de Nyquist no gráfico gerado pelo MATLAB.
Antes de usar , vamos entrar com no MATLAB usando a função . Lembra dela? Ela tem como entrada dois vetores com os coeficientes dos polinômios do numerador e do denominador da função de transferência. Repare que o denominador de está fatorizado em parte. Logo, para podermos pegar os coeficientes dele, precisamos expandi-lo (isto é, multiplicar os termos) para gerarmos o polinômio. Por isso, antes de usarmos , faremos uma manipulação algébrica com o denominador de .
Passo 2
Para obter o polinômio do denominador de , vamos multipicar seus termos usando o MATLAB. Em um novo script, digite as linhas de código:
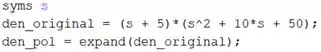
Na primeira linha, criamos uma variável simbólica .
Na segunda linha, entramos com o denominador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará o polinômio que precisamos, armazenando-o em .
Rodando o programa, temos:

Passo 3
Agora que temos o polinômio do denominador de , podemos criar os vetores que servirão de entrada para . Lembrando que que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Para , o polinômio do numerador é . Já o polinômio do denominador é .
Em um novo script ou no script onde você obteve , vamos criar duas variáveis representando os coeficientes dos polinômios, para servirem de entrada para . Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de, indo do elemento com maior expoente ao de menor expoente:

Logo abaixo, já incluimos o comando para criar , que será armazenado na variável .
É bom dar uma conferida em antes de continuar. Para isto, rode o programa que você tem até agora e imprima no Command Window:

Estando tudo nos conformes, podemos partir para o próximo passo, que é plotar o diagrama de Nyquist.
Passo 4
Para plotar o diagrama de Nyquist, use a função , que tem como sintaxe:
Ela tem como entrada uma função de transferência, criada usando o comando do MATLAB (representada por acima), e ela gera um gráfico com o diagrama de Nyquist para .
Adicione em seu código o comando:
![]()
Execute o programa e você terá o diagrama de Nyquist de :
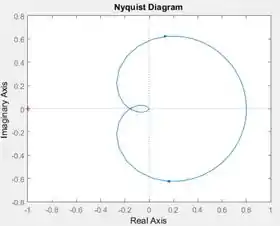
Passo 5
Com o diagrama de Nyquist em mãos, podemos avaliar a estabilidade do sistema usando o critério de Nyquist, que é dado pela equação:
Onde:
- é o número de polos positivos da função de transferência em malha fechada;
- é o número de voltas que o diagrama de Nyquist dá em torno de . é positivo se a volta for no sentido horário. Se for no sentido anti-horário, é negativo.
- é o número de polos positivos da função de transferência em malha aberta.
Pelo critério de Nyquist, para que um sistema seja estável, deve ser igual a .
O é obtido calculando as raízes do denominador da função de transferência em malha aberta, no caso, . Para isto, é mais fácil a gente pegar o dado diretamente no enunciado, onde os termos do denominador não foram multiplicados:
Neste exercício, o denominador de é e tem três raízes. A primeira raiz é fácil de achar: é . Para encontrar as duas raízes restantes, do polinômio de grau , vamos usar a função do MATLAB, que tem como sintaxe:
Ela tem como entrada o vetor , que contém os coeficientes do polinômio cuja raízes queremos encontrar, indo do elemento com maior expoente ao de menor expoente. O comando retorna as raízes do polinômio e as armazena em .
No nosso exercício, queremos encontrar as raízes de . Logo, o vetor é:
Vamos adicionar no nosso script do MATLAB o comando para acharmos as raízes:
![]()
Executando o programa, temos que as raízes de são dois números complexos:

Logo, as três raízes do denominador são , e . Quando temos zeros que são números complexos, avaliamos a parte real do número. Como a parte real das raízes e é negativa, , não tem polos positivos e .
Passo 6
é obtido pelo diagrama de Nyquist. Vamos rever o diagrama de Nyquist gerado no passo :

Tem uma cruzinha vermelha na extremidade esquerda do gráfico, reparou? Essa cruzinha marca o ponto de coordenadadas . Como a cruzinha está fora do diagrama de Nyquist (que é a curva azul com flechinhas), o diagrama não dá volta alguma em torno de , logo,
Tendo e , calculamos . Temos que . Como , o sistema é estável.
Resposta
Sistema estável