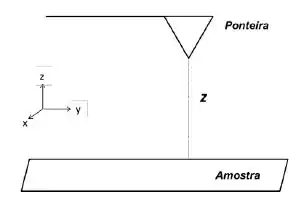
Um aparato bastante utilizado em Nanotecnologia é o microscópio de força atômica, que permite medir a força de interação entre a superfície da ponteira e a superfíce de uma amostra em escala nanométrica. Dentre os modelos usados para descrever essa interação está um variante do potencial Lennard-Jones, conhecido como potencial , cuja forma funcional é dada abaixo:

Onde é a distância entre a ponteira e a amostra, e são parâmetros do potencial, com unidades de energia distância, respectivamente, com e .

Bom, como ele quer equilíbrio, temos que a força precisa ser , ok? Então agora que já temos uma expressão pra força, vamos usar ela pra ver quando ela vale 0

Isolando o ficamos:

Como ele quer a energia em um determinado ponto e eles nos deu a expressão da energia, é só nós aplicarmos o ponto que queremos na função da energia.

Lembrando:

Substuindo agora o nosso zezin

Pelo que percebemos na letra a descobrimos as faixas de valores em que a Força é positiva e a Força é negativa.

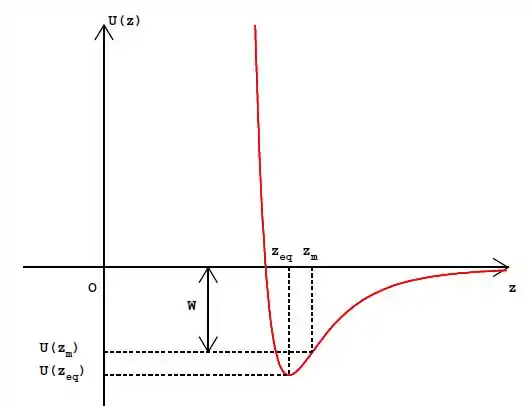
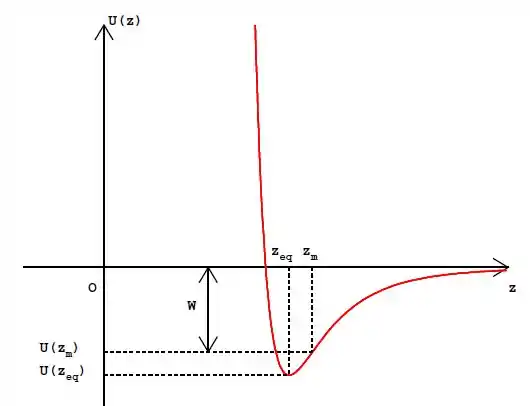
Ok, mas e os pontos de equilíbrios? Bom, a gente descobriu que só tem 1 só, certo? Se a gente pegar qualquer valor de , tanto a esquerda quanto a direita, podemos ver que o potencial será maior que o nosso ponto de equilíbrio, ou seja, estamos tratando de um equilíbrio estável!

É igual uma montanha russa, que nem a gente viu lá nos tipos? Se fizer o gráfico do potencial, fica tipo isso aqui.

O ponto onde a força é nula nós já encontramos, certo? É o nosso ponto de equilíbrio

Agora o ponto onde ela é mínima ... vamos ter que derivar mais uma vez pra achar os extremos da força, ok?

Igualando essa expressão a temos:

Sendo assim:

Para calcular o trabalho realizado, podemos usar a expressão de potencial para calcular a diferença de potencial entre os pontos que ele pede. Como ele quer da distância em que a força é mínima até um ponto infinito, temos:

Onde

Como o é denominador na expressão do potencial, temos que = 0, ou seja: