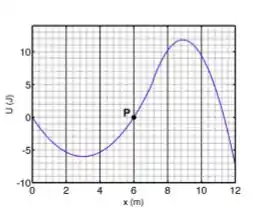
Uma partícula é lançada em com energia cinética , viajando ao longo do eixo horizontal e submetida a uma forca horizontal cuja energia potencial é conhecida (veja gráfico). A partícula pode se mover somente ao longo do eixo e não existem forças dissipativas.
Assinale a alternativa correta:
(a) O trabalho necessário para levar a partícula de até só pode ser determinado se conhecermos a massa da partícula.
(b) A energia cinética da partícula no ponto depende do tempo que a partícula permanece no potencial.
(c) A partícula tem energia suficiente para alcançar a posição .
(d) O trabalho necessário para levar a partícula da origem até o ponto de equilíbrio estável é positivo.
(e) O ponto é um ponto de retorno.
(f) A velocidade da partícula em é nula.
(g) A força exercida sobre a partícula no ponto é positiva
Passo 1
Vamos analisar uma alternativa por vez:
a) Falsa. Sabemos que:
Como conseguimos a variação da energia potencial pelo gráfico, teríamos o trabalho realizado pela força direto.
Passo 2
b) Falsa. A energia cinética depende somente da variação da energia potencial.
Passo 3
c) Falsa. A energia cinética inicial é de , portanto, a máxima variação da energia potencial é de . Como no ponto a energia potencial é de , a partícula não chegará lá.
Passo 4
d) Verdadeira. O ponto de equilíbrio estável está com energia potencial , como:
Passo 5
e) Falsa. O ponto é um ponto com energia potencial nula. Um ponto de retorno é definido como o ponto onde a energia cinética é nula.
Passo 6
f) Falsa. Até o ponto , a partícula ganha mais energia cinética e portanto, mais velocidade, já que a energia potencial é negativa.
Passo 7
g) Falsa. Sabemos que:
Como a derivada no ponto é positiva, a força é negativa.
Resposta
Letra (d)