Uma partícula de massa move-se em uma dimensão ao longo do eixo e de acordo com a energia potencial, em , dada por:
a) Esboce o gráfico de , para
b) Encontre a força associada a esta energia potencial
c) Ache a(s) posição(ões) de equilíbrio, e identifique-o(s) como instável, estável ou indiferente. Justifique sua resposta.
d) Qual é o valor de no ponto de equilíbrio instável?
e) Supondo que a partícula esteja inicialmente em repouso no ponto de equilíbrio estável de , qual é a mínima velocidade que se deve dar a ela para que seu movimento deixe de ser confinado?
Passo 1
a)
Se colocarmos o em evidência:
Podemos encontrar os pontos onde a função .
Temos então as raízes:
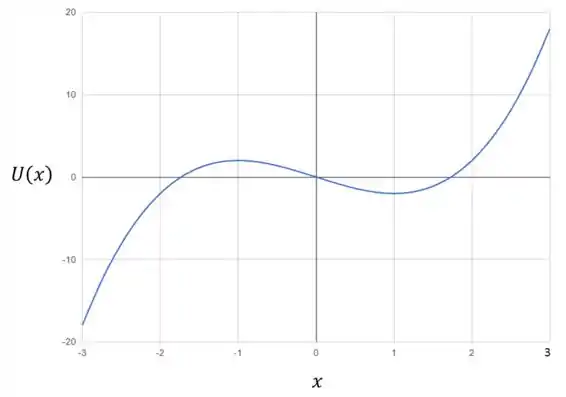
Como a função é um polinômio, dá para montarmos o gráfico da função apenas com as raízes. Vai ficar:

Passo 2
b)
Basta utilizar a fórmula:
Passo 3
c)
As posições de equilíbrio ocorrem onde . Logo:
Observando o gráfico conseguimos identificar que a posição é um ponto de equilíbrio instável (pico de um morro) e a posição é um ponto de equilíbrio estável (um vale).
Passo 4
d)
Basta fazer a substituição:
Passo 5
e)
O movimento deixará de ser confinada se a partícula conseguir alcançar o ponto de equilíbrio instável com um infinitésimo de velocidade. Pois se isso acontecer ela vai sair do equilíbrio e se afastar cada vez mais no sentido de negativo.
Vamos calcular a diferença de energia entre os pontos de equilíbrio instável e estável. Já calculamos o valor de no equilíbrio instável no item acima.
Para o equilíbrio estável:
Logo, a diferença entre as energias é:
Ou seja, para que a partícula saia do confinamento, ela precisa receber mais que de energia. Agora é só utilizar a fórmula da energia cinética:
Resposta
a)
b)
c) : equilíbrio instável; : equilíbrio estável.
d)
e)