Seja um subespaço vetorial do . (Projeções e reflexões desta questão são ortogonais.) Diga se as afirmativas abaixo são verdadeiras ou falsas.
- A transformação obtida primeiro projetando em e depois refletindo em torno de é diferente da transformação obtida primeiro refletindo em torno de e depois projetando em .
- A reflexão de em torno de é dada pela fórmula , onde denota a projeção em .
é falsa e é verdadeira
Ambas são falsas
Ambas são verdadeiras
é verdadeira e é falsa
Passo 1
Afirmativa :
Essa afirmativa que é aparentemente muito difícil, mas se lembrarmos daquela imagem fica fácil:
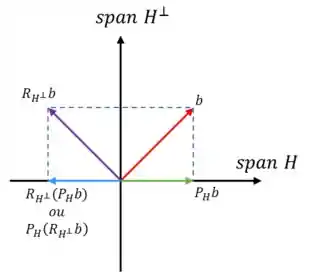
Lembra dela? Eu modifiquei um pouquinho pra se adequar ao problema, mas no fundo é a mesma imagem! Como podemos ver, qualquer caminho que escolhamos vamos chegar no mesmo resultado! Uma coisa interessante de trabalharmos com complementos ortogonais é que, como talvez vocês já tenham percebido, podemos usar o para representar qualquer espaço na hora de verificarmos alguma afirmação ;)
Logo, essa afirmativa é falsa, já que ta dizendo que é diferente.
Passo 2
Afirmativa :
Novamente, eu peguei aquele desenho que mostrei pra vocês e dei uma mexida nele:
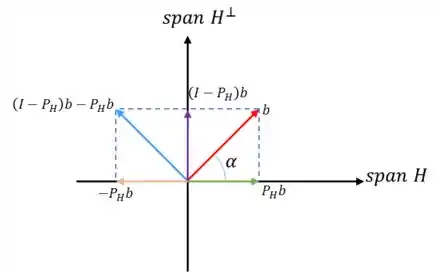
Podemos ver que a reflexão de por é dada por:
Se substituirmos por :
Logo, essa está correta!
Resposta
Letra