Uma caixa hermética, cuja tampa tem uma área de , é parcialmente esvaziada. A força necessária para abrir a caixa vale e a pressão atmosférica é igual a . Calcule a pressão no interior da caixa.
Passo 1
No problema, uma caixa é parcialmente evacuada, ou seja, a sua pressão interna diminui. Além disso, alguém está tentando abri-la. Tudo isso gera uma composição de forças, como veremos. Nossa missão é encontrar a pressão interna da caixa.
Passo 2
Sendo:
: a força necessária para abrir a caixa, feita por uma pessoa, e que vale .
: a força gerada pela pressão atmosférica, que ainda vamos calcular.
: a força gerada por aquela tal pressão interna que queremos descobrir.
: pressão atmosférica, de (utilizando .
pressão interna.
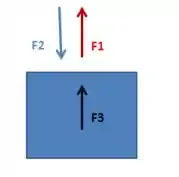
A distribuição espacial das forças fica conforme a figura:
Primeiramente, devemos calcular as forças. Pelo enunciado, apenas a força exercida pela pessoa foi dada. Usaremos a relação a seguir para calcular as outras:
Logo, e valem:
E o valor de já é conhecido (:
Agora, estamos preparados para equacionar e descobrir .
Passo 3
Bom, a figura da distribuição espacial das forças nos mostra que e apontam para cima, enquanto aponta para baixo. A lógica nisto é que a força gerada pela atmosfera precisa ser “vencida” para que a caixa abra. Portanto, devemos igualar a soma das forças que apontam para cima a para que, após isso, isolemos :
Sendo , e , basta aplicar na equação e obteremos:
Resposta