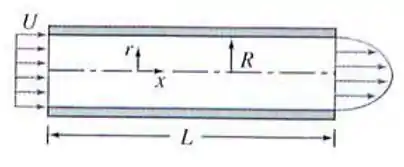
Água escoa em regime permanente através de um tubo de comprimento e raio . Calcule a velocidade de entrada uniforme, , se a distribuição de velocidade através da saída é dada por e
Passo 1
O primeiro passo para resolver qualquer problema de escoamento é listar as características do escoamento que você conhece.
Nesse caso, o nosso escoamento é permanente então:
E incompressível já que o fluido é água. Ser incompressível significa que os fluxos de entrada e de saída de água devem ser iguais.
Assim, pelo que vimos na teoria, se há conservação de massa a equação que usamos é:
Isso para um volume de controle qualquer. Então vamos escolher o nosso de forma a nos ajudar, isso quer dizer com forma e posição fixa. E que as superfícies que atravessam o escoamento façam com o escoamento.
Assim:
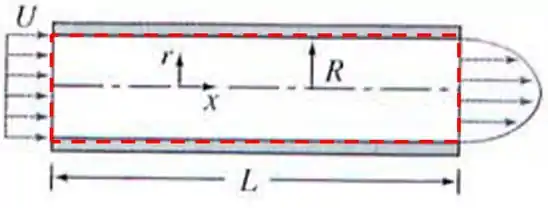
E a equação fica sendo:
Nesse caso , sendo e
Passo 2
Hora de atacar!
Vamos começar colocando as constantes para fora da integral:
Então podemos cortar aquele que apareceu dos dois lados:
Vamos resolver primeiro o lado direito, a integral de é só mesmo:
Passando o para o outro lado e substituindo a área:
Agora, vamos usar uma propriedade das integrais, que a soma de integrais é igual a integral da soma:
Resolver a primeira integral é tranquilo:
Agora, só falta resolvermos a integral difícil, vou até deixar pra outro passo.
Passo 3
Como e não são independentes, não podemos simplesmente tirar o da integral como fizemos antes. A área é a área de um círculo, assim podemos abrir em:
Assim, nossa integral vai virar uma integral de a .
Agora essa integral ficou mais simples, já que temos apenas um polinômio:
Substituindo os limites, temos que a nossa integral é igual a:
Passo 4
Voltando agora a nossa equação temos:
Como é então podemos cortar e , chegando assim:
Assim, chegamos no resultado final, bastando substituir o valor de