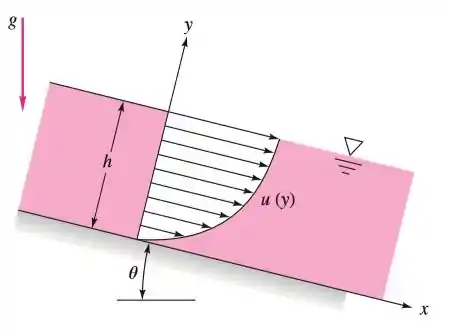
Uma fina camada de líquido escorrendo sobre um plano inclinado, como na figura abaixo, terá um perfil de velocidades laminar, , em que é a velocidade na superfície. Se o plano tem largura normal ao papel, determine a vazão volumétrica do filme. Suponha que e que a vazão para cada metro de largura do canal seja de . Calcule em .
Passo 1
Essa questão é para treinarmos a questão de escolher o volume de controle.
Qual dos dois você acredita ser o melhor? O vermelho ou o azul?
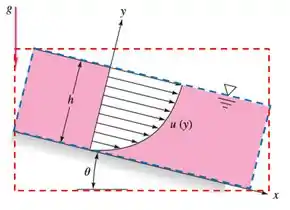
O vermelho está certinho no eixo , sem nenhuma inclinação, porém ele engloba só o liquido e ainda, o liquido escoa pelo volume de controle fazendo um ângulo .
Agora o volume de controle azul, esse está inclinado igual o escoamento, sendo assim engloba apenas o fluido escoando e esse fluido ainda escoa fazendo com a superfície de controle o que já vimos que é muito bom.
Não tem problema inclinarmos o volume de controle, pelo contrario, isso ajuda muito quando o escoamento está inclinado.
Então vamos usar esse volume de controle azul.
Passo 2
Agora vamos calcular o que o enunciado pediu que foi a vazão.
Onde e
Colocando as constantes para fora da integral.
Agora temos duas integrais de polinômio para fazer,
Substituindo agora os limites de integração, temos:
Passo 3
Mas o que queremos é , como temos a vazão podemos substituir na equação da vazão que encontramos. Porém essa unidade de vazão está escrota. Vamos passar para .
Sabemos que e .
Assim, temos:
Agora, podemos substituir na equação que encontramos: