Um aluno realizou um experimento onde colocava um certo bloco em cima de uma mesa para calcular o efeito que a massa tinha na compressão das pernas da mesa.
Devido a repetidos experimentos ele obteve os seguintes dados experimentais:

Utilize os dados experimentais para encontrar o polinômio que melhor se ajusta aos dados experimentais.
Passo 1
A questão é uma aplicação direta do segundo método para criação de polinômios, ele deu dois vetores de dados e pede para encontrar o polinômio que melhor se ajuste aos dados experimentais.
Para isso iremos precisar criar um código que além de gerar a função também gere uma saída de dados gráfica para que possamos comprar os dados com o polinômio para ver se a curva realmente se ajusta bem:
Para isso vamos realizar o seguinte algoritmo:
- Entrada de dados ( inserir os vetores dado da questão)
- Programação do ajuste utilizando a função
- Criação de uma saída de dados para comprar o polinômio com os dados experimentais.
Passo 2
Transformando o algoritmo em programação no Matlab vamos inserir os seguintes pontos:
Primeiramente vamos inserir vetores de dados:
Agora vamos inserir a função para o cálculo do polinômio:
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a criação dos seguintes elementos de código:
Criação de um vetor para a variação contínua da curva e a criação da própria curva:
Agora vamos criar o plot:
O código em Matlab deve ficar algo mais ou menos assim:

Após variar a ordem do polinômio foi visto que o polinômio que melhor se ajusta com menor ordem possível é o polinômio de grau 3, sendo assim o gráfico do polinômio de grau 3 fica:
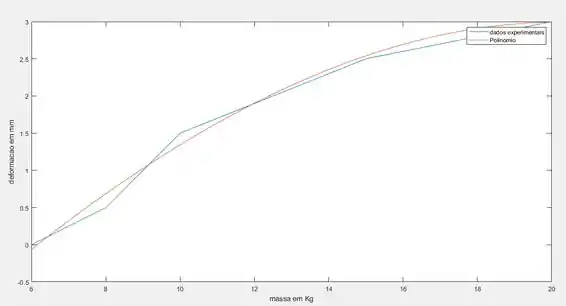
Cujo os coeficientes são dados pelos seguintes valores:
![]()
Resposta
O polinômio que melhor se ajusta é o polinômio: