Plote o polinômio:
No domínio . Primeiramente crie um vetor. Em seguida, utilize a função para terminar os valores de e por fim, empregue a função .
Passo 1
A questão quer que a gente plote o gráfico de um polinômio utilizando a função , pois pede para calcular o valor do polinômio sob todos os valores dentro do intervalo dado.
Se temos um intervalo é mais simples trabalhar operações sobre vetores pois temos infinitos números dentro daquele intervalo. Uma vez que criamos o vetor com os elementos daquele intervalo que foi dado (em x), podemos calcular a função sob o vetor para ter todos os seus valores (em y). Para uma melhor visualização, vamos plotar os resultados em uma imagem gráfica.
Então o algoritmo para a resolução desse problema é o seguinte:
1-Entrada de dados – Criação do vetor X e do polinômio na forma vetorial
2- Cálculo do polinômio utilizando a função
3-Gerar o gráfico com o comando plot.
Passo 2
Primeiramente vamos inserir os coeficientes do polinômio.
Lembrando que os termos que não aparecem no polinômio, nós trocamos por 0 no vetor, então como não aparece a potência cúbica, o polinômio fica assim:
A justificativa de ficar assim é a mesma mostrada em aula, utilizando álgebra básica podemos mostrar que o polinômio da questão pode ser obtido através da multiplicação das seguintes matrizes:
E os coeficientes correspondem justamente a matriz .
Agora vamos criar o Vetor .
o incremento foi escolhido 0.1 de forma arbitrária para conter o maior número possível de elementos que correspondam aos valores do intervalo fornecido na questão.
Agora vamos inserir a função para o cálculo dos polinômios:
Uma vez que criamos as funções vamos gerar a saída de dados que corresponde a:
Passo 3
O código em Matlab deve ficar algo mais ou menos assim:
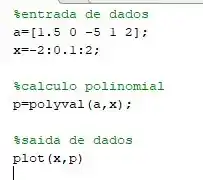
Executando o código iremos obter o seguinte resultado:

Resposta
Ei, a resposta está no passo a passo :)