Dados os polinômios:
A soma é igual a?
Passo 1
Aqui temos uma questão bem padrão de polinômios, o enunciado pede para calcular o valor do polinômio para o valor de e seguidamente pede para calcularmos o valor de para valor de e finalmente somar esses valores para ter o resultado final.
Para resolver a questão primeiramente precisamos inserir os vetores dos coeficientes de cada polinômio. Uma vez que implementamos, vamos utilizar a função que é uma função que serve para calcular os valores dos polinômios para algum valor de
Sendo assim, o algoritmo do nosso programinha ficaria:
1-Implementação dos vetores dos coeficientes dos polinômios P e Q
2-Cálculo dos polinômios nos valores especificados de X
3-Cálculo da soma de P e Q
Passo 2
Agora que já montamos nosso algoritmo vamos implementá-lo na forma de código no Matlab.
Nossa primeira linha será composta pelos vetores dos coeficientes dos polinômios P:
Lembrando que o apareceu simplesmente porque não tem o coeficiente do no polinômio P, por isso colocamos o valor nulo quando vamos implementar no Matlab.
De forma similar temos o polinômio Q:
Passo 3
Agora que implementamos os coeficientes dos vetores precisamos apenas calcular os valores dos polinômios com a função polyval. Primeiro entramos com o polinômio e depois o valor de x.
Agora vamos implementar a função da soma para assim resolver a questão em sí:
Passo 4
Resultado o seguinte codigozinho:

Executando o código:
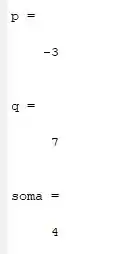
Resposta
Executando o código você irá encontrar os seguintes valores para o polinômio e consequentemente a soma: