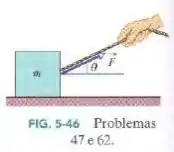
Na Fig. 5-46, um bloco de massa é puxado ao longo de um piso horizontal sem atrito por uma corda que exerce uma força de módulo e ângulo . (a) Qual é o módulo da aceleração do bloco? (b) O módulo da força é aumentado lentamente. Qual é o seu valor imediatamente antes de o bloco perder contato com o piso? (c) Qual é o módulo da aceleração do bloco na situação do item (b)?
Passo 1
Temos aqui uma situação onde forças agem em um bloco, onde temos como dados:
- Massa do bloco;
- Valor das forças que agem nele
E nos é pedido a aceleração desse bloco. O que podemos fazer? Vamos usar a segunda lei de Newton! Que relaciona exatamente o que temos com o que queremos.
Passo 2
Primeiramente vamos fazer o Diagrama de Corpo Livre, atentando para a existência da força normal. No diagrama também já faremos a decomposição da força na direção normal dos eixos e .
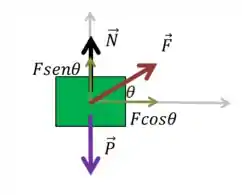
Se aplicarmos agora a segunda lei de Newton independentemente para cada eixo. No eixo , temos:
Substituindo os valores de e , chegamos ao seguinte valor para :
Já no eixo , temos:
Aqui esbarramos em um problema. Nós não temos o valor nem de e nem de , portanto, essa equação não teria solução. No entanto, como sempre na física, buscaremos argumentos físicos para encontrar valores de coisas que a gente não sabe. Perceba que a jogada que vamos usar aqui dará spoiler para a solução da letra (b), se liga:
Concorda que, se o corpo tivesse aceleração vertical pra cima, ou seja, se fosse diferente de 0, a primeira coisa que aconteceria seria o corpo perder contato com o chão? E concorda também que se existisse essa perda de contato, a normal se tornaria nula? Então vamos lá: se a componente vertical de , , for maior ou igual ao peso, ela será grande o suficiente para tirar o corpo do chão e acarretar em tudo que foi perguntado.
Já que temos o valor da componente vertical e o valor do peso, podemos descobrir qual é essa relação!
Certo, então o peso é maior que a componente vertical e o corpo permanece no chão, com isso, concluímos que, nessas condições:
Para responder a letra (a), vamos então usar os resultados obtidos:
Passo 3
Com o spoiler que demos na letra (a), a gente consegue descobrir de cara o que temos que fazer para descobrir módulo da força quando o corpo começa a perder o contato com o solo. Precisamos também observar que neste momento, o corpo continua sem aceleração vertical. Para matar o item, basta fazer a força normal e a aceleração em ser zero! Portanto, aplicando a segunda lei novamente no eixo , temos:
E entã, substituindo os valores conhecidos, temos:
Passo 4
Já usamos na letra (b) que a aceleração vertical no instante em que o bloco perde o contato com o chão é nula, portanto, para acharmos o módulo da aceleração, basta acharmos a aceleração no eixo . Aplicando a segunda lei no eixo encontramos:
Substituindo o valor de e usando o valor de que encontramos na letra (b), temos:
Já confirmamos que a aceleração nesse instante é horizontal, portanto: