Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método dos Coeficientes Indeterminados – Soma de Funções

Ver Teoria
Exercício 1412345678910111213

Enunciado

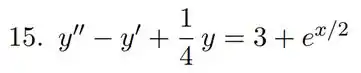
Passo 1

Caso de EDO homogênea. Vamos lá! Precisamos resolver

y ' ' - y ' + 1 4 y = 3 + e x 2

Para começar, vamos resolver a equação como se fosse homogênea. Ignorando essa coisa toda que tá do lado direito.

y ' ' - y ' + 1 4 y = 0

Para isso vamos determinar a equação característica

r 2 - r + 1 4 = 0

Encontrando as raízes teremos

∆ = 1 - 1 = 0

r = 1 2

Então a solução homogênea é:

y h x = C 1 e x 2 + C 2 x e x 2

Passo 2

Agora precisamos encontrar a solução particular, infelizmente não dá pra ignorar aquele lado direito da equação para sempre.

Nesse caso temos uma soma de funções

3 + e x 2

Então precisamos supor soluções particulares para ambas as funções.

y p 1 = a x + b

Atenção! Lembra que e x 2 já apareceu na nossa solução homogênea. Então precisamos multiplicar a função por x até que ela fique diferente do que já apareceu:

y p 2 = x 2 e x 2

A solução particular será a soma dessas soluções

y p = a x + b + c x 2 e x 2

Passo 3

Para encontrar as constantes a , b   e   c precisamos derivar a solução particular que chutamos e substitui-la na EDO. Então teremos

y p = a x + b + c x 2 e x 2

y p ' = a + 2 x c e x 2 + c x 2 e x 2 2

y p ' ' = 2 c e x 2 + x c e x 2 + c x e x 2 + c x 2 e x 2 4

y p ' ' = 2 c e x 2 + 2 c x e x 2 + c x 2 e x 2 4

Substituindo na nossa EDO

y ' ' - y ' + 1 4 y = 3 + e x 2

2 c e x 2 + 2 c x e x 2 + c x 2 e x 2 4 - a - 2 x c e x 2 - c x 2 e x 2 2 + a x 4 + b 4 + c x 2 e x 2 4 = 3 + e x 2

8 c e x 2 + 8 c x e x 2 + c x 2 e x 2 - 4 a - 8 x c e x 2 - 2 c x 2 e x 2 + a x + b + c x 2 e x 2 = 12 + 4 e x 2

8 c e x 2 + 8 c x e x 2 - 8 x c e x 2 + c x 2 e x 2 - 2 c x 2 e x 2 + c x 2 e x 2 + a x + b - 4 a = 12 + 4 e x 2

a x + b - 4 a + 8 c e x 2 = 0 x + 12 + 4 e x 2

Juntando os termos semelhantes, encontramos

a = 0

b - 4 a = 12

8 c = 4

Logo:

a = 0 b = 12 c = 1 2

Então a solução particular fica

y p ( x ) = 12 + x 2 2 e x 2

Passo 4

Sabemos que

y x = y h x + y p ( x )

E

y h x = C 1 e x 2 + C 2 x e x 2

y p ( x ) = 12 + x 2 2 e x 2

Então

y x = C 1 e x 2 + C 2 x e x 2 + 12 + x 2 2 e x 2

Resposta

y x = C 1 e x 2 + C 2 x e x 2 + 12 + x 2 2 e x 2

Exercícios de Livros Relacionados

Encontre a solução geral da equação diferencial u ' ' + ω 0 2 u = c o s ω t Com ω 2≠ ω 0 2
Em cada um dos problemas de 15 a 20, encontre a solução do problema de valor inicial dado. y ' ' + 4 y = 3 sen ⁡ 2 t , y 0 = 2 , y ' 0 = - 1
Em cada um dos problemas de 1 a 14, encontre a solução geral da equação diferencial dada. u ' ' + ω 0 2 u = cos ⁡ ω 0 t
Encontre a solução geral da equação diferencialy^(' ') + 2 y^' + y = 2 e^(- t)
Encontre a solução geral da equação diferencialy^(' ') + y^' - 2 y = 2 t y (0) = 0 , y^' (0) = 1