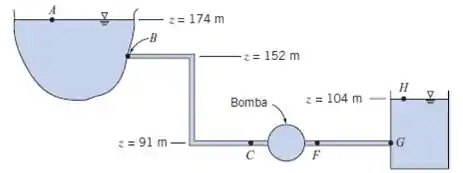
(Adaptada) Um grande reservatório fornece água para a comunidade. Uma parte do sistema de abastecimento de água é mostrada. A água é bombeada de um reservatório para um grande tanque de armazenagem antes de ser enviada para a instalação de tratamento de água. O sistema é projetado para fornecer 1310 L/s de água a 20°C. De B para C, o sistema consiste em uma entrada da borda-viva, 760 m de tubo, três válvulas gaveta, quatro cotovelos de 45° e dois cotovelos de 90°. Todo o tubo é de ferro fundido de 508 mm de diâmetro e fator de atrito 0,017. Calcule a perda localizada no trecho BC.
Passo 1
Para calcular a perda localizada, uma das opções é calcular assim:
é o coeficiente de perda localizada de cada acidente e a velocidade do fluido que passa pelo obstáculo.
Porém, repara que nesse exercício, o diâmetro é de 508 mm e que não foi dito se é flangeado ou rosqueado. Nesse caso, o uso da tabela que temos dos coeficientes K só ajuda para calcular a parte da entrada, cujo K conhecemos e é 1. E para os outros acidentes?
Relaxa que esse caso tem solução! Temos informação sobre o fator de atrito e a tabela de comprimentos equivalentes para cada acidente dito no enunciado. Isso vai nos ajudar muito!
E com isso, vamos usar a seguinte fórmula:
Como a tubulação tem o mesmo diâmetro no trecho BC e mesmo material, f e V são os mesmos para todos os acidentes:
Precisamos conhecer a velocidade V e os de cada obstáculo. Começando pela velocidade:
Como o duto é circular, a área é:
Substituindo os valores e convertendo a vazão para o m³/s:
Logo, a velocidade é
Passo 2
Fazendo uma lista dos acidentes que ocorrem no trecho BC:
- 1 entrada da borda-viva
- 3 válvulas gaveta
- 4 cotovelos de 45°
- 2 cotovelos de 90°
Pela tabela a seguir, encontramos os valores de para cada acidente.

Lembrando que para a entrada sabemos que o K é 1. Substituindo na equação da perda localizada
Show! Encontramos a perda de carga localizada.