Uma tubulação de aço comercial tem 5 m de comprimento e 13 mm de diâmetro. Água escoa a 0,2 L/s passando por uma válvula globo rosqueada totalmente aberta e um cotovelo de 90° normal rosqueado. Calcule (a) a perda de carga global, (b) a perda de carga localizada e (c) compare os valores e analise qual tipo de perda é mais significativo nesse trecho.
Passo 1
Olá! Nesse exercício vamos relacionar os dois tipos de perda que aprendemos. Daqui para frente vamos sempre estar atentos a eles.
Sobre a perda de carga global , aprendemos que ela depende do comprimento da tubulação, do diâmetro, da velocidade do tubo e do fator de atrito
Vamos primeiro calcular essa velocidade, pois vamos usar esse valor ao longo de todo o exercício, já que o diâmetro da tubulação permanece o mesmo.
Sendo um tubo circular, a área é:
Substituindo o que conhecemos do enunciado e passando a vazão para o m³/s:
Assim encontramos a velocidade:
Passo 2
Para o cálculo da perda global, falta conhecer o fator de atrito. Esse cálculo depende se o escoamento é laminar ou turbulento. Então vamos analisar Reynolds.
Considerando que o fluido é a água, substituímos
Como Reynolds é maior que 2300, então o escoamento é turbulento. Logo, o fator de atrito depende de Reynolds e da rugosidade relativa .
Falando nela... Sendo o tubo de aço comercial, pela tabela de rugosidade, .
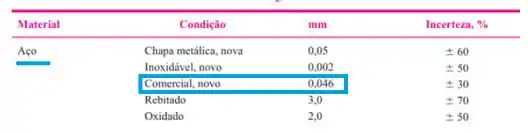
Com e , usamos o Diagrama de Moody
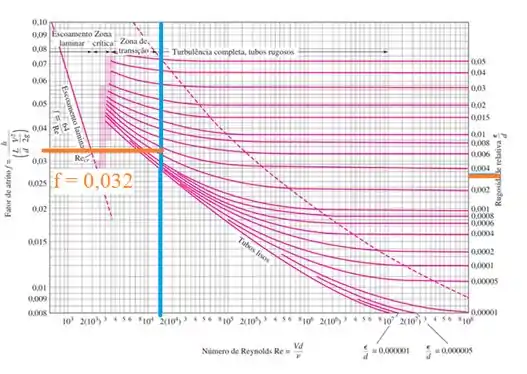
O fator de atrito é aproximadamente 0,032 como indicado no zoom.
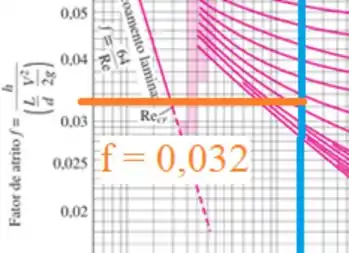
A reta laranja não está traçada exatamente na curva de 0,004 de rugosidade relativa, pois o valor mais preciso é 0,0035. Por isso, foi marcada um pouco abaixo. Beleza?
Agora vamos substituir os valores para encontrar a perda de carga:
Passo 3
Até aqui, encontramos a perda de carga global. Vamos analisar a letra b, que pede a perda localizada:
é o coeficiente de perda localizada de cada acidente e a velocidade do fluido que passa pelo obstáculo.
Como todos os acidentes estão num trecho de mesmo diâmetro, então a velocidade é a mesma que já calculamos.
Ok! Para encontrar os coeficientes de perda localizada, vamos fazer uma lista dos obstáculos que o fluido passa:
- 1 válvula globo totalmente aberta
- 1 cotovelo de 90° normal
Vamos encontrar na tabela. O diâmetro é 13 mm e são acidentes rosqueados
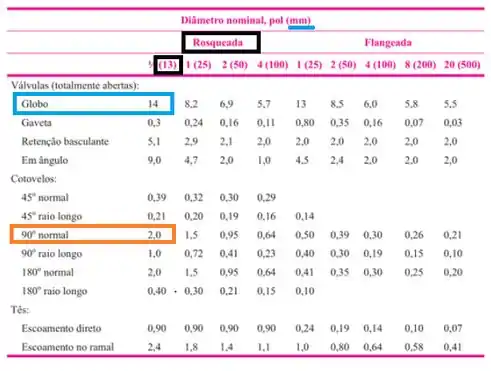
Assim, pela tabela encontramos que:
Calculando a perda localizada:
Substituindo:
E assim encontramos a perda localizada!
Passo 4
Finalmente, vamos a letra c, fazer uma comparação
O escoamento nas condições apresentadas nesse exercício tem perda global (causada pelo escoamento do fluido ao longo da tubulação) de 1,43 m e perdas localizadas (causadas pelos acidentes) de 1,86 m.
Então, nesse caso, a perda localizada é maior que a perda global, a perda localizada é mais significativa. Beleza, ok... Mas o que isso quer dizer?

Por exemplo, se quiséssemos atuar para diminuir as perdas desse trecho, seria interessante atuar nos obstáculos e trocá-los por outros que tenham um coeficiente de perda localizada menor! Isso teria mais impacto do que trocar o material do tubo, por exemplo.
É muito importante lembrar que se a situação fosse outra (outro material da tubulação, outro comprimento, outros acidentes), a perda de carga global poderia ser mais significativa. Para fazer essa afirmação de quem é mais significativa, precisamos analisar cada escoamento, ok? o/