Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Perdas localizadas e Dutos não-circulares

Ver Teoria
Exercício 61234578

Enunciado

A Figura mostra um ensaio de perdas para um filtro espesso. A vazão no tubo é de 7   m 3 / m i n e a pressão a montante é de 120   k P a . O fluido é o ar a 20 ° C . Usando a leitura do manômetro de coluna de água, estime o coeficiente de perda K do filtro.

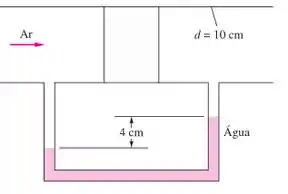
Passo 1

Calma galera, sei que parece um pouco diferente, mas é um exercício parecido com o que estamos fazendo, ou seja:

Bora montar a equação da energia! (só não grita de emoção, pode atrapalhar os coleguinhas do lado)

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p + h p l

Vamos então cancelar os termos que não variam da entrada para a saída:

-Não varia a altura do duto:

z 1 = z 2

-Não varia a vazão nem a área, logo não varia a velocidade:

V 1 = V 2

-Vamos supor que as perdas globais h p são desprezíveis.

Nossa equação fica com a seguinta cara então:

p 1 ρ g = p 2 ρ g + h p l

Passo 2

Agora as coisas mudam um pouquinho, pois temos essa perda local h p l = K V ² 2 g do filtro.

Vamos colocar esse valora na equação:

p 1 ρ g = p 2 ρ g + K V ² 2 g

Arrumando as coisas:

K = 2 p 1 - p 2 ρ V 2

Beleza então precisamos calcular os termos ρ ,   V e p 1 - p 2 .

Lembra daquela expressão de gases perfeitos p = ρ R T ?

Podemos aproximar o ar como um gás perfeito para calcular sua massa específica, ou consultamos alguma tabela que tenha os valores para p = 120   k P a e T = 20 ℃ .

Logo

ρ = p R T

T = 20 ℃ = 293   K   e

  R = 287   J / ( K g . K )

ρ = 120 × 10 3 287 × 293 = 1,43   k g / m ³

A velocidade podemos calcular pela vazão Q = 7   m ³ / m i n e pela área A = π 4 d ²

V = Q A = 7 60 π ( 0,1 ) ² 4

V = 14,85   m / s

Agora podemos olhar o manômetro para calcular a pressão na saída p 2 .

Se lembrarmos lá do início da Hidrostática, podemos fazer um balanço de pressões:

p 1 + ρ a r g h - ρ á g u a g h = p 2

Se reorganizarmos isso veremos que o termo p 1 - p 2 aparece:

p 1 - p 2 = - ρ a r g h + ρ á g u a g h

Logo

p 1 - p 2 = - ρ a r + ρ á g u a g h

p 1 - p 2 = - 1,43 + 998 × 9,81 × 0,04

p 1 - p 2 = 391   P a

Substituindo tudo na expressão de K :

K = 2 391 1,43 × 14,85 2

K = 2,479

Resposta

K = 2,479

Exercícios de Livros Relacionados

Quando lidamos com a lubrificação de rolamentos, a equação de governo que descreve a pressão é a equação de Reynolds, geralmente descrita em uma dimensão como: d d x h 3 μ . d p d x + 6 U . d h d x =
Uma grande massa é suportada por um pistão de diâmetro D = 100m m e comprimento L = 100m m . O pistão está assentado em um cilindro fechado no fundo. A folga a = 0,025m m entre a parede do cilindro e
A distribuição de velocidade em uma fina película de fluido escoando para baixo sobre uma superfície inclinada foi desenvolvida no Exemplo 5.9. Considere um filme de 7 mm de espessura de um líquido co
Um mancal de deslizamento selado é formado por cilindros concêntricos. O raio interno e o externo são 25 e 26 mm, respectivamente, o comprimento do mancal é 100 mm, e ele gira a 2800 rpm. A folga radi
O perfil de velocidade para escoamento completamente desenvolvido de óleo castor a 20 °C entre placas paralelas em movimento, é dado pela Eq. 8.8. Considere U = 1,5m / s e a = 5m m . Determine o gradi