Uma bola é mantida em repouso na posição A por meio de dois fios ideais, como mostra a figura.
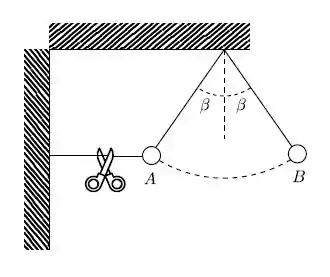
O fio horizontal é cortado, e a bola começa a oscilar como um pêndulo. O ponto é o ponto mais afastado do lado direito da trajetória das oscilações. O atrito com o ar é desprezível. A razão entre a tensão do fio na posição e a tensão do fio na posição antes do fio horizontal ser cortado está dada por
Passo 1
Se liga! Vamos começar decompondo as forças na posição A.
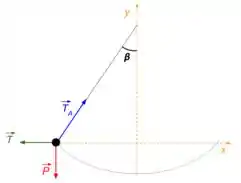
Levando em consideração que enquanto o fio lateral não for cortado a corda permanece em equilíbrio, podemos dizer que
Fazendo a decomposição de nas componentes em e , temos
Passo 2
Agora podemos ver o que acontece na posição B. Se liga na figura.
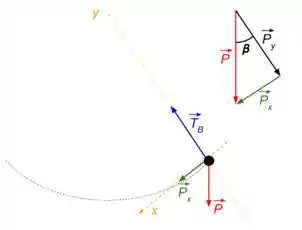
Repara que modificamos as nossas coordenadas para facilitar as contas. Na posição B não há equilíbrio. Existe uma força resultante na direção , tal que
Já no eixo , temos
Portanto
Passo 3
Agora só precisamos calcular a razão
Portanto a resposta correta é a letra (a).