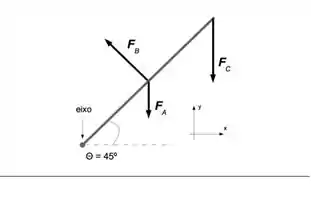
Uma haste, submetida às forças indicadas na figura, está presa a um eixo fixo em uma das suas extremidades. Sabendo-se que a haste pode girar livremente (isto é, o atrito com o eixo é desprezível) e que , podemos dizer que a resultante das forças que agem sobre a haste será zero se a força aplicada pelo eixo na haste for tal que:
(a) suas componentes e são ambas positivas.
(b) sua componentes e são ambas negativas.
(c) sua componente é nula e sua componente é igual à componente de .
(d) sua componente é positiva e sua componente é nula.
(e) sua componente é negativa e sua componente é antiparalela à componente de .
Passo 1
Inicialmente fazemos a decomposição da força nos eixos, bem como a força , aplicada no eixo, supondo os sentidos ilustrados a seguir, que serão corrigidos através dos cálculos.
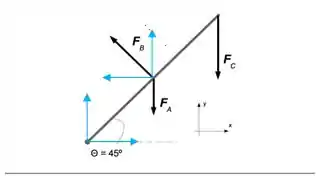
Passo 2
Para que a resultante das forças sobre a barra seja nula, deve existir equilíbrio de forças tanto em quanto em .
Para o equilíbrio na direção :
Como os módulos são iguais, o sentido da componente horizontal de deve ser oposto ao de , certo? Então, temos que sua componente em deve ser positiva.
Passo 3
Para o equilíbrio na direção :
De acordo com a relação fornecida pelo enunciado:
Ao substituir essa relação na anterior:
Logo, a componente em da força será também positiva.
Resposta
(a)