Você está em pé em uma balança em um elevador de um edifício. Sua massa é de . O elevador começa do repouso e se movimenta verticalmente para cima com uma velocidade que varia com o tempo de acordo com a equação . Quando qual a leitura da balança?
Passo 1
Eaeeee, belezinha??? Seguinte... temos que colocar na cabeça que a balança lê a massa equivalente pela força normal e não pela força peso (geralmente dizemos que uma é igual a outra, mas nem sempre ein).
Dessa forma, precisamos descobrir qual a força normal em para podermos obter a massa que está sendo lida pela balança!!
E aí??? Bora responder??!!
Passo 2
Sabemos que a aceleração é a derivada da velocidade. Dessa forma, temos:
Pata , temos:
Passo 3
Fazendo o diagrama do corpo livre do sistema, vemos:
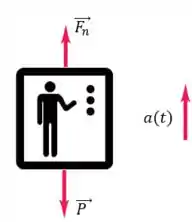
Pela 2ª Lei de Newton, temos:
Passo 4
Assim, a massa lida pela balança é dada por:
Entendeu direitinho? Responde aee ;)
