UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 4d
4. Considere uma vasilha semiesférica de raio (conforme a figura acima à direita). Um cubo de gelo de massa cai da borda da vasilha (desconsidere o atrito).
d) Qual o módulo da velocidade do cubo de gelo no ponto assinalado na figura?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão a situação é a seguinte: temos uma vasilha semiesférica de raio e na borda dessa vasilha cai um cubo de gelo de massa . Com isso, queremos obter a velocidade do cubo de gelo no ponto da figura.
Parece complicado, não é? 😐
Novamente podemos usar a lei de conservação de energia. Como não há atrito do gelo com a vasilha, a energia se conservará em todos os instantes.
Isso quer dizer que toda a energia gravitacional do cubo no momento em que ele está na borda é convertida para energia cinética.
Sacou? Bora começar! 😎
Passo 2
Perceba que no ponto o cubo de gelo possui energia potencial gravitacional e energia cinética, ou seja, se a energia potencial é calculada como
No ponto inicial a energia é dada por
Já no ponto temos a seguinte situação
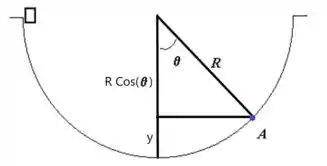
A altura será dada pelo valor de .
Nesse caso, é a distância completa e é a parte acima de , então podemos escrever que .
Tranquilo até aqui? 😉
Passo 3
Com isso, podemos dizer que a energia potencial do cubo no ponto é dado por
E por fim, a energia cinética no ponto será dada por
E pela lei da conservação de energia, a energia do sistema no ponto é igual a energia do sistema no início.
Simplificando a equação...
Fim! Iae, o que achou? Responde Aí! 😁
