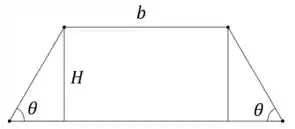
Uma piscina no formato de um trapézio isósceles tem sua área dada pela fórmula . Abaixo, uma representação dessa piscina:
Use diferenciais para aproximar o erro no cálculo de se (exatamente), (exatamente) e com erro possível de .
Além disso, determine o erro percentual no cálculo de .
Passo 1
Bem, aqui ele quer um aproximação do erro de e o erro percentual desse mesmo . Vamos começar achando o erro de , para isso vamos achar seu diferencial em relação a :
Podemos trocar o valor de e de nessa fórmula já que ele é constante:
O seu diferencial vai ser:
Por fim:
Passando para direita:
Passo 2
Agora que temos o diferencial, sabemos, pela teoria, que podemos relacionar com , e vai ser o erro na conta. Assim:
Além disso, também sabemos que pode ser aproximado por . Ele deu a variação de , então temos:
Esse é o intervalo do erro, vamos passar esses valores dos ângulos para radiano, porque sempre que trabalhamos com ângulo precisamos usar radianos:
Assim vamos ter:
Multiplicando isso por , vamos ter:
Assim, aquele cara do meio é :
Ele disse o valor de , que vai ser , vamos passar isso para radianos:
Assim, temos:
Ufa, achamos o intervalo do erro dessa área. Vamos recapitular o que fizemos. Achamos a fórmula da diferencial de , que vai ser o erro que ele está querendo. Depois nos achamos o intervalo que o erro de vai estar. Depois fizemos umas contas para chegar no intervalo de , que é só ir multiplicando a função no valor de que for o ponto inicial, ou ponto central.
E pronto temos o nosso intervalo.
Passo 3
Vamos agora achar o erro percentual dessa parada, para isso temos que achar o erro relativo, que é a mesma coisa
Então precisamos achar o valor de no valor inicial de
Já sabemos o intervalo de , então basta dividir geral nesse intervalo por , que achamos o erro relativo
Fazendo essa conta na calculadora vamos ter:
Passando para porcentagem e substituindo por vamos ter o erro percentual variando entre: