Um professor um pouco pirado entregou pra seus alunos o gráfico da curva e pediu para que calculassem a área abaixo do gráfico entre e . Os alunos optaram por calcular essa área usando um triângulo retângulo cuja hipotenusa tangenciasse a curva. Abaixo, uma representação de como esse triângulo muda em função do ponto de tangência:
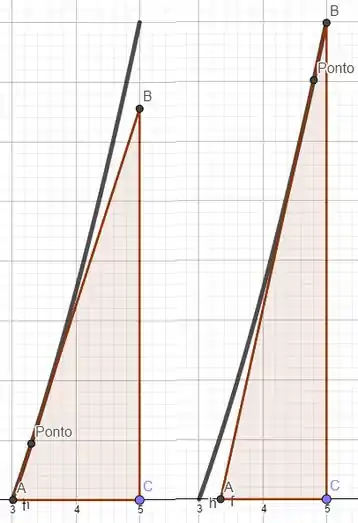
Sabendo que os alunos escolheram como ponto de tangência e que o erro na marcação desse ponto é de calcule o erro percentual no cálculo de . Depois, calcule também o mesmo erro em relação à área real abaixo da curva.
Passo 1
Bem, aqui ele quer um aproximação do erro de e o erro percentual desse mesmo . A nossa dificuldade nessa questão vai ser achar a expressão de em função de uma variável pra podermos variar. De qualquer forma, a área do retângulo vai ser:
Mas quem vai ser a base e a altura? Pô, o truque pra tirar de letra quem vai ser e é lembrar que a hipotenusa desse triângulo é uma reta tangente, e retas tangentes tem a seguinte expressão:
Onde é o ponto de tangência na curva . Escolhendo um ponto de tangência qualquer , vamos ficar com:
Esse nada mais é do que a inclinação da reta tangente no ponto de tangência, lembra? Então a gente calcula ele tranquilin assim ó:
E a equação da reta tangente é reescrita para:
Como a altura desse triângulo está sempre, pela figura, em cima de , temos que:
Show, falta achar a base agora. Se a gente olhar pro esquema do enunciado vemos direitinho que a base vai ser sempre “menos algo”. E olha só! Não é que esse “algo” vai ser sempre o valor de em que a reta tangente toca o eixo ? Sendo assim, a base vai ser:
A base vai ser então:
E a área vai ser:
Passo 2
Nesse passo, vamos fazer o diferencial, beleza? Já que , o diferencial vai ficar:
Passando pro outro lado:
Agora que temos o diferencial, sabemos, pela teoria, que podemos relacionar com , e vai ser o erro na conta. Assim:
Além disso, também sabemos que pode ser aproximado por . Ele deu a variação de , então temos:
Multiplicando isso por , vamos ter:
Assim, aquele cara do meio é :
Ele disse o valor de , que vai ser , segundo o enunciado, a gente substitui:
Assim, temos:
Passo 3
Vamos agora achar o erro percentual dessa parada, para isso temos que achar o erro relativo, que é a mesma coisa
Então precisamos achar o valor de no valor inicial de , que é
Já sabemos o intervalo de , então basta dividir geral nesse intervalo por , que achamos o erro relativo
Passando para porcentagem e substituindo por vamos ter o erro percentual variando entre:
Graficamente da pra ver que a área desse triângulo não é muito diferente da área abaixo da curva, saca só:
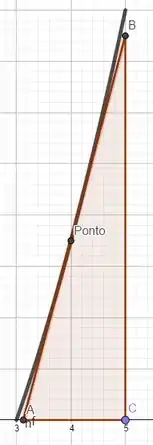
Se usássemos como no calculo do erro relativo a área real, teríamos que fazer:
O erro relativo seria:
E por fim:
Resposta
Em relação à área calculada pelos alunos:
Em relação à área real: