Um corpo de massa sai do repouso e cai em queda livre de uma altura com relação ao solo. Quando ele passa pela altura (veja a figura abaixo) é desviado por um anteparo de modo que assume uma nova velocidade na horizontal tal que o módulo dessa velocidade é igual ao módulo da velocidade que o corpo tinha imediatamente antes de ser desviado.
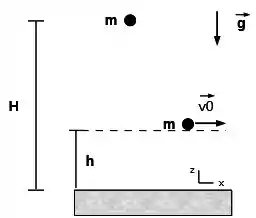
Ache o vetor velocidade com que o corpo é lançado na horizontal.
A que distância de sua posição inicial o corpo atinge o solo?
Quais valores de dariam o mesmo alcance ?
Qual valor de maximiza ?
Note que para uma função , o valor que maximiza esta função é obtido tomando a derivada com relação a e igualando a zero de forma que .
Passo 1
Bem primeiramente precisamos encontrar o vetor velocidade na altura , que pelas fórmulas de movimento uniformemente variado pode ser encontrado por:
Entretanto precisamos do instante de tempo em que o corpo chega a altura , para isso vamos utilizar outra fórmula de MUV:
Substituindo os valores e lembrando que o corpo parte do repouso, portanto , encontramos:
Agora podemos isolar o tempo para encontrar o instante em que ele chega a altura :
Agora já temos o tempo para substituir na nossa fórmula:
Lembrando que no instante inicial.
Onde é o versor que indica a direção e sentido da velocidade (vertical para baixo). Ainda podemos simplificar essa expressão jogando a gravidade para dentro da raiz:
Muito bem, mas o problema quer o vetor com que o corpo é lançado na horizontal após chocar-se com o anteparo. Que segundo o enunciado possui o mesmo módulo de , logo:
Passo 2
O alcance pode ser calculado pela fórmula:
Onde o é o tempo de voo, que a gente não possui ainda. Mas a gente pode descobrir usando a seguinte fórmula para o eixo :
Onde nós sabemos que o e que , além de que pois ele inicia um novo movimento na altura onde inicial é zero. Agora vamos substituir:
Isolando o tempo , temos:
Agora podemos substituir na nossa fórmula do alcance:
Lembrando que corresponde a velocidade inicial em que encontramos no item anterior.
Passo 3
Bem, no item anterior encontramos , note que se abrirmos essa equação ficamos com:
Logo, vemos que depende de quadraticamente, quer dizer, podem existir dois valores de para o qual essa raiz dê . Para simplificar nossa vida, vamos elevar ao quadrado os dois lados da equação, porque ai podemos sumir com essa raiz chata.
Muito bem, caímos numa equação do segundo grau, basta calcular as raízes que são:
Essas duas raízes fornecem dois valores de para o qual o alcance é .
Passo 4
Para descobrirmos o no qual o alcance é máximo, vamos seguir a dica do exercício.
Derivando a equação vamos encontrar:
Logo, para que essa divisão seja zero, o numerador precisa ser zero, portanto: