Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Projeção em Base Ortogonal

Ver Teoria
Exercício 171234567891011121314151618192021222324

Enunciado

UFRJ, Álgebra Linear, P3 – 2017.2, Questão 01

Sejam u → ,   v →   ∈ R 4 tais que a projeção ortogonal de u → na direção de v →   é igual a ( 1 ,   1 ,   2 ,   2 ) . O vetor u → pode ser qualquer um dos abaixo, COM EXCEÇÃO DE:

(a) ( 3 ,   1 ,   2 ,   1 )

(b) ( 4 ,   2 ,   1 ,   1 )

(c) ( 3 ,   2 ,   1 ,   1 )

(d) ( 3 ,   1 ,   1 ,   2 )

Passo 1

O que acontece aí é isso:

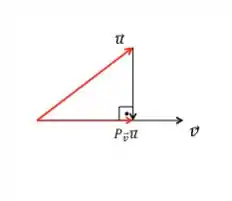
Conseguimos ver que a projeção e esse vetor entre o u → e a projeção formam um ângulo reto entre si.

Reparem que esse vetor é simplesmente P v → u → - u → . Então:

P v → u → - u → , P v → u → = 0

Queremos saber qual desses vetores das opções pode ser o vetor u → sendo que sabemos que a projeção é   P v → u → = ( 1 ,   1 ,   2 ,   2 ) . Vamos testar para cada um esse produto interno nulo!

Passo 2

a)   u → = ( 3,1 , 2,1 )

P v → u → - u → = 1,1 , 2,2 - 3,1 , 2,1 = ( - 2,0 , 0,1 )

Vamos ver se o produto interno de fato vale zero.

P v → u → - u → , P v → u → = - 2,0 , 0,1 , ( 1,1 , 2,2 ) = - 2 + 2 = 0

Sim, logo, essa não é a exceção!

b)   u → = ( 4,2 , 1,1 )

P v → u → - u → = 1,1 , 2,2 - 4,2 , 1,1 = ( - 3 , - 1,1 , 1 )

Vamos ver se o produto interno também vale zero.

P v → u → - u → , P v → u → = ( - 3 , - 1,1 , 1 ) , ( 1,1 , 2,2 ) = - 3 - 1 + 2 + 2 = 0

Sim, logo, essa também não é a exceção!

c)   u → = ( 3,2 , 1,1 )

P v → u → - u → = 1,1 , 2,2 - 3,2 , 1,1 = ( - 2 , - 1,1 , 1 )

Vamos ver se o produto interno também vale zero.

P v → u → - u → , P v → u → = ( - 2 , - 1,1 , 1 ) , ( 1,1 , 2,2 ) = - 2 - 1 + 2 + 2 = 1

Diferente de 0 ! Então essa era a exceção que estávamos buscando!

Resposta

Letra c

Exercícios de Livros Relacionados

19. Encontre os vetores w → 1 em W e w → 2 em W ⊥ tais que x → = w → 1 + w → 2 com x → e W dados no(a) Exercício 14(a)(b) Exercício 15(a)
15. Os vetores dados são ortogonais com produto interno euclidiano. Encontre p r o j W x → , com x → = 1,2 , 0 , - 2 e W o subespaço de R 4 gerado pelos vetores dados.(a) v → 1 = 1,1 , 1,1 , v → 2 = 1
14. Os vetores dados são ortogonais com produto interno euclidiano. Encontre p r o j W x → , com x → = 1,2 , 0 , - 2 e W o subespaço de R 4 gerado pelos vetores dados.(a) v → 1 = 1,1 , 1,1 , v → 2 = 1
Verifique se os seguintes pontos pertencem a um mesmo plano:A = (2, 2, 1), B = (3, 1, 2), C = (2, 3, 0) e D = (2, 3, 2);A = (2, 0, 2), B = (3, 2, 0), C = (0, 2, 1) e D = (10, −2, 1)
Decomponha W = - i → - 3 j → + 2 k → como a soma de dois vetores W1 e W2, com W1 paralelo ao vetor j → + 3 k → e W2 ortogonal a este último. (Sugestão: Revise o Exemplo 3.10 na página 178).