Calcular o fluxo do campo vetorial
através da superfície orientada pelo vetor noraml tal que .
Passo 1
Só de olhar já da pra ver que com esse campo aí, calcular a integral pelo método direto ia ser impossível, né? Pensamos então no teorema da Gauss.
No entanto, se você for observar a superfície, notamos que ela n é fechada, logo, vamos ter que arrumar outra superfície para poder fechar isso aí e podermos aplicar o teorema de Gauss, tranquilo?
O que antes seria
Agora vai virar
Vamos lembrar de observar que S e precisam ter a orientação certinha para os vetores normais apontarem pra fora de V, tranquilo?
Passo 2
Temos ainda um segundo poré. Observa que nosso campo tem uma singularidade quando e são iguais a zero. Lembra que não podemos trabalhar com divisão por zero, certo?
Então não podemos fechar a superfície aberta com um disco, pois ele passaria pela origem, e não podemos permitir que nossa superfície passe pelo ponto onde existe a singularida.
Vou te passar uma manha aqui salvador. Observa que no denominador, a função que da problema é
Isso pode ser um indicador para usarmos isso. La na frente, quando a gente for parametrizar a jogar no campo, isso daí vai simplificar demais nosso denominador. Então façamos
Confia, haha.
Passo 3
Pra a gente entender agra em qual direção o vetor normal vai ter que apontar em casa superfície, preciso que você perceba que fica por cima do hemisfério , então o volume V que vamos calcular, está limitado por cima de e por baixo de
Quando a gente for usar Gauss, precisamos que a normal esteja para cima de , e a normal para baixo em
Com essa orientação, ficamos com
Passo 4
Bora então calcular logo esse divergente aí
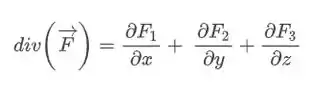
Onde
Podemos então resolver a integral triplea
Passo 5
Maravilha! Aora vamos partir para a parte da integral de superfício na sup
Começamos parametrizando a mesma.
O vetor normal (com a orientação certa) fica
Podemos então montar a integral e resolver
Observa agora que temos ali um maroto no denominador. Bora fazer uma mudança pra coordenadas polares, onde nosso raio fica variando entre zero e 1, e dando a voltinha completa
Substituição simples
Passo 6
Podemos agora então voltar pra nossa igualdade.
Lembrando que o enunciado não nos pediu
Mas sim
Sendo que
Logo