Sejam
E parte do paraboloide , com , orientada com . Calcule:
Passo 1
O enunciado nos pede uma integral de superfície que parece bem complicada de se resolver, principalmente pela complexidade do campo . Para tentar simplificar isso ai, vamos aplicar o Teorema de Gauss, o enunciado dele é esse aqui:
Essa questão aqui tem uma peculiaridade, o campo , vamos então ter que fazer tudo para o campo primeiro e depois para o campo . No primeiro vamos ter que remover uma singularidade e no segundo não, por isso facilita dividir o campo nesses dois casos.
Passo 2
Nosso campo tem denominador, né? Então ele tem uma singularidade. Nesse caso, o ponto que o denominador é zero é a origem . Portanto, além de fechar nossa superfície, vamos ter que remover a singularidade do sólido com uma terceira superfície! Essas duas tem que ser simples de calcular, se não for, não adianta nada tudo isso.
Nosso esboço vai ser esse aqui:
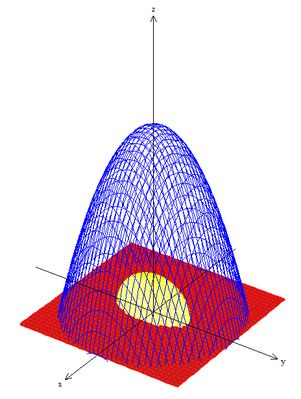
Perceba que usamos o próprio plano para fechar o paraboloide.
Além disso, usamos um elipsoide para remover a origem do sólido.
Mas de onde você tirou esse elipsoide pra tirar a origem?? Calma, eu falei que precisamos escolher com muita atenção as superfícies, né? Esse termo aparece exatamente igual no campo . Quando formos calcular a integral dessa superfície vai ficar tudo bem simples, prometo!
Pelo teorema de Gauss:
Só para deixar bem explícito, a superfície é o plano e a superfície é o elipsoide. Vamos fazer tudo isso passo a passo bem devagar, vamos lá?
Passo 3
Vamos começar pela integral tripla. Você lembra como calcula o divergente de um campo? É essa fórmula aqui:
Lembrando que o nosso campo é a soma de dois campos:
Ta vendo que o termo aparece exatamente igual nas 3 derivadas? Ele vai apareces multiplicado por na nossa soma.
Além disso, o termo aparece multiplicado cada vez por um termo em cada derivada, certo? Vamos colocá-lo em evidência na soma. Fica assim:
Somando os expoentes:
Que beleza né! Não vamos nem precisar calcular a integral tripla!
Passo 4
Vamos para a integral da superfície , o plano , sua parametrização vai ser:
Nesse caso, o cálculo da normal vai ser feito assim:
Só lembre-se que a normal, para o teorema de Gauss, tem que estar apontando para fora do sólido, nesse caso queremos negativo, portanto a normal correta é:
Substituindo na integral de superfície:
Como isso é um produto escalar, vai dar exatamente zero!
Passo 5
Vamos para a nossa outra integral, a da superfície , que é o elipsoide . Sua parametrização é a seguinte:
Os limites são esses porque só queremos metade do elipsoide, então não vai de a . Vamos escrever com os novos parâmetros, lembrando que escolhemos esses valores justamente para o nosso denominador ficar igual a , portanto:
Nossa normal vai ser dada por:
Vamos ver se a nossa orientação está certa, para perceber isso pegue algum ponto, por exemplo e , nesse caso o valor da normal é:
Veja que, graficamente, a nossa normal deve apontar para fora do sólido , certo? Então, nesse caso, nossa orientação da normal é negativa mesmo!
Pronto! Agora vamos calcular a nossa integral, substituindo , a normal e os limites de integração:
Integrando em
Integrando em
Passo 6
Voltando para o Teorema de Gauss:
Passo 7
Fizemos tudo isso para o nosso campo com a singularidade, né? Vamos ter que fazer algo semelhante para o segundo campo, mas fica tranquilo que esse é mais rápido, só de não ter singularidade facilita muito!
Nosso esboço vai ficar bem parecido, só não vamos precisar do elipsoide, então vai ficar assim olha:
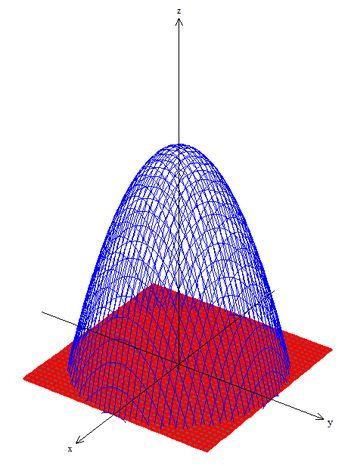
Pelo Teorema de Gauss:
Passo 8
Vamos começar pelo divergente de novo:
Para calcular a integral tripla, temos que descobrir os limites do nosso sólido. Para calcular isso, vale a pena fazer uma mudança cilíndrica nas variáveis. Portanto:
está limitado pelo paraboloide e pelo plano , com isso:
O paraboloide projetado no eixo fica:
Que é uma circunferência de raio , portanto:
Definidos os limites, agora só resta calcular a integral!
Passo 9
Agora precisamos calcular a integral de superfície do plano , para isso, a parametrização da superfície vai ser:
Só que, como , nosso campo escrito com os novos parâmetros fica assim:
Portanto, como o fluxo é nulo, nem precisamos calcular a normal, o valor da integral de superfície com certeza é zero!
Passo 10
Voltando para o Teorema de Gauss para o campo :
Passo 11
Finalmente, juntando as integrais de superfície que calculamos para e ficamos com:
