Calcular a transformada de Laplace da função definida por
Passo 1
Precisamos de um esboço para escrevermos como função degrau. O gráfico dessa função é um negócio assim:
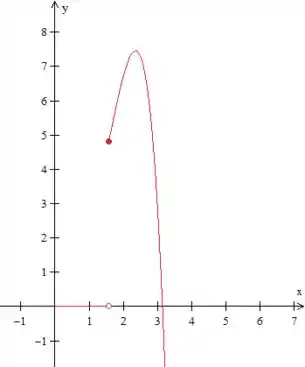
Você sabia disso? Pois é, eu também não, acabei de descobrir : ) A verdade é que não precisamos saber como é a função , só precisamos saber onde ela começa, para podermos raciocinar.
Então, vamos usar um desenho qualquer para essa função, ok? Pois não fazemos ideia de como ela seja:
Passo 2
Agora vamos escrever como função degrau. Como temos uma função que vale até e passa a valer a partir de , podemos escrever o seguinte:
Isso quer dizer que:
Pronto, isso que queremos!
Passo 3
Agora vamos calcular , como o problema pediu. Temos o seguinte:
Aplicando para o nosso problema:
Precisamos, então, achar . Temos o seguinte:
Então, para encontrarmos temos que somar onde tem :
Como :
Assim, temos:
Passo 4
Precisamos agora resolver essa expressão. Vamos rearrumar isso aqui:
Sabemos do seguinte:
Como temos uma exponencial multiplicando o cosseno, essa transformada será deslocada. Vamos usar a seguinte fórmula:
Substituindo esse valor, temos: