São dados as retas e o plano e o ponto
a) Determine a posição relativa entre e .
b) Determine a projeção do ponto sobre a reta .
c) Determine a projeção do ponto sobre o plano .
d) Determine o ângulo entre a reta e a reta .
Passo 1
a) O vetor diretor de é e o vetor normal do plano é
Vamos testar o produto interno entre eles:
Beleza, se o produto interno é 0, quer dizer que a reta é perpendicular ao vetor normal do plano, ou sejaa: é paralela ao plano ou está contida nele.
A gente tem que descobrir se ela é paralela (estando láá longe do plano) ou se ela ta dentro dele, pra isso a gente vai substituir algum ponto da reta na equação de .
Se der uma igualdade verdadeira, a reta ta contida no plano, caso contrário, ela só é paralela mesmo.
Passo 2
Da equação da reta, a gente sabe que o ponto pertence a ela, então vamos substituir esse ponto na equação do plano:
Boaaa, deu uma igualdade verdadeira!!
Isso quer dizer que todos os pontos de também estarão no plano , logo, está contida em .
Passo 3
b) vai ser um ponto da reta que vai satisfazer a seguinte projeção:
Ou seja, o vetor vai ser a projeção de no vetor , que é o vetor diretor de .
Ficou difícil de enxergar isso? Vamo ver na imagem
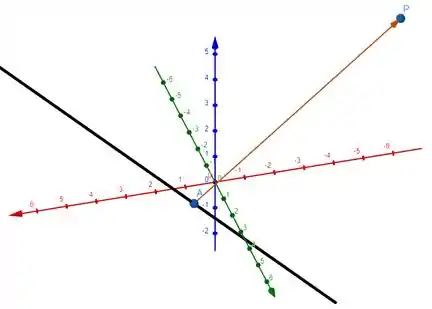
A reta é a preta e o vetor laranja é . A projeção desse vetor em vai ser , sendo que é o ponto que a gente ta procurando ;)
Passo 4
Beleza, então vamo fazer a tal da projeção
Sabemos que , então:
Então
Passo 5
c) Vamos imaginar uma reta que passe pelo ponto e seja paralela ao vetor normal do plano .
A intersecção dessa reta com o plano vai ser o ponto que estamos procurando.
A equação paramétrica dessa reta é
Pra encontrar a intersecção da reta com o plano, vamos substituir seu , e na equação do plano :
Substituindo na equação de , teremos que o ponto de intersecção vai ser
Passo 6
d) A gente ta querendo o ângulo entre e
Sabemos que . Pra calcular o ângulo entre eles vamos fazer o produto vetorial:
Opa, o produto vetorial entre e é 0. Isso quer dizer que o ângulo entre eles é :)
Resposta
a)
b)
c)
d)