Calcular a distância do ponto à reta
Passo 1
O exercício nos pede para calcular a distância entre um ponto e uma reta. Com a equação da reta fornecida conseguimos tirar as seguintes informações:
Dados:
Vimos como calcular diferentes distâncias na teoria! Não lembra, como calcula entre ponto e reta?! Vamos relembrar!!

Passo 2
Quando queremos a distância entre ponto e reta, sempre temos que ter em mente a seguinte figura:
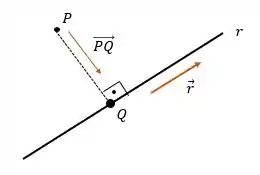
Nós temos o ponto e temos o vetor diretor da reta . O próximo passo é determinar o ponto genericamente. Para isso, vamos escrever primeiro a equação vetorial da reta :
Assim, é:
Sabendo o jeitão de podemos determinar o vetor :
Passo 3
Temos da equação da reta que e descobrimos que Sabemos da teoria que o vetor diretor da reta e o vetor são ortogonais, logo:
Calculando:
Agora que achamos que podemos calcular :
Passo 4
Estamos quase terminando!! Agora, para acharmos a distancia entre o ponto e a reta , é só calcular a distância entre os ponto e
Substituindo os valores: