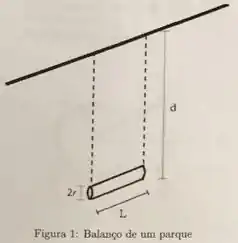
Um balanço de parque é formado por uma barra cilíndrica de massa , raio , e comprimento , preso por fios de massa desprezível a um eixo fixo superior, paralelo ao eixo da barra cilíndrica, conforme a figura 1. A barra pode girar em torno desse eixo fixo. O centro da barra está a uma distância do eixo. O momento de inércia da barra com relação ao eixo fixo vale:
Dados de Momento de inércia:
Disco uniforme (massa , raio )com relação a um eixo que passa pelo seu centro de massa e é perpendicular ao plano do disco: .
Barra uniforme (massa , comprimento ) com relação ao eixo que passa pelo seu centro de massa e é perpendicular ao comprimento da barra: .
(A)
(B)
(C)
(D)
(E)
Passo 1
Para encontrar o momento de inércia do cilindro com relação a esse eixo temos duas opções.
A primeira seria montar uma integral cabulosa e calcular na mão...

Bom, qualquer coisa que eu falar agora vai ser melhor que isso né?
O segundo e melhor jeito é usar um valor de momento de inércia tabelado e adaptá-lo para o eixo do problema.

Passo 2
Mas como vamos adaptar?
Basta aplicar o Teorema dos eixos paralelos:
Mas para isso, precisamos que o eixo seja paralelo com o do problema.
Passo 3
No formulário, temos o eixo passando pelo disco seria um caso assim:
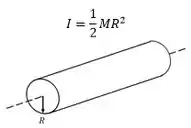
Ué, mas isso é um cilindro...
Exatamente, um cilindro nada mais é do que um disco prolongado, seus momentos de inércia são iguais.
Em contrapartida, o eixo que passa perpendicular ao comprimento do cilindro é um caso assim:
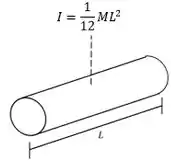
Então, vamos usar o primeiro caso, o do eixo passando paralelamente ao comprimento.
Passo 4
Então, aplicando o teorema, temos:
Onde será a distância entre os eixos:
Resposta
Letra (A)