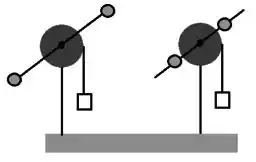
Cada sistema e é composto de um disco, uma haste presa ao disco e duas massas presas `a haste. A haste está contida no plano do disco. Um bloco é preso à extremidade livre de um fio leve enrolado ao redor do disco que pode girar livremente em torno do eixo que passa pelo seu centro e é perpendicular ao seu plano. Os dois sistemas mostrados na figura abaixo são idênticos, exceto pelas posições das massas na haste. Se os dois blocos são soltos simultaneamente a partir do repouso, qual deles chega primeiro ao solo? E por que?
O do sistema , porque neste o momento de inércia é maior do que o de .
O do sistema , porque neste o momento de inércia é menor do que o de .
O do sistema , porque neste o momento de inércia é menor do que o de .
O do sistema , porque neste o momento de inércia é maior do que o de .
Os dois blocos chegam ao mesmo tempo.
Passo 1
Para determinar que bloco chega primeiro no solo, devemos determinar qual sistema possui menor momento de inércia, pois sabemos que:
Como o torque é o mesmo, temos que quanto menor , maior será a aceleração angular!
Pensando nos dois sistemas, temos que possui menor , pois pelo teorema dos eixos paralelos, temos que as massas das haste contribuem com:
Como no sistema , a distância entre as massas e o centro de massa é menor, temos que o momento de inércia será menor!
Portanto, o sistema faz com que o bloco chegue mais rápido ao solo, pois apresenta um menor momento de inércia.
Resposta