Um disco metálico homogêneo de raio tem um furo circular de raio conforme a figura abaixo.
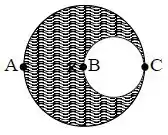
Três eixos paralelos entre si e perpendiculares ao disco passam pelos pontos , e da figura. A posição do centro de massa é representada por um na figura.
Os momentos de inércia do objeto em relação a cada um desses eixos são, respectivamente, , e .
Determine a alternativa correta:
- ;
- ;
- ;
- ;
- ;
- .
Passo 1
Bem, dada a beleza contemporânea desse disco, se tem algo que eu NÃO quero fazer é ter que calcular o momento de inércia dele em relação a , e . Bem, realmente ele não pede isso em nenhum lugar.
Todas as respostas estão comparando os momentos de inércia! Bem, isso dá pra gente fazer. Vamos usar o teorema dos eixos paralelos.
Esse teorema nos diz que, sendo o momento de inércia com relação a um eixo que atravessa o centro de massa do corpo, o momento de inércia com com relação a um eixo paralelo a esse e que passe por um ponto qualquer vai ser:
Onde é a distância entre os dois eixos.
Isso significa que podemos comparar , e usando a distância deles até o centro de massa!
O momento de inércia varia diretamente com a distância do ponto até o centro de massa. Além disso, comparando os três, eles só serão diferentes nessa distância.
Nesse caso, pela figura, temos que , onde a distância é maior que a distância devido ao fato de o centro de massa ser ligeiramente deslocado em direção a .
Assim teremos:
Que corresponde à letra (e)
Resposta
Letra (e)