Uma haste longa e fina de massa e comprimento é livre para girar sobre um ponto localizado a de seu comprimento. A haste é posicionada na posição horizontal, como mostrado na figura , por um fio preso na extremidade:
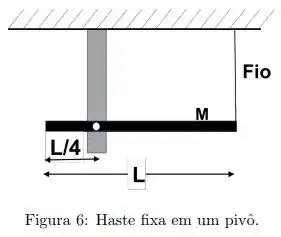
(a) Dado que o momento de inércia em relação ao eixo de rotação perpendicular a haste e passando pelo centro de massa é , determine o momento de inércia da haste relativo ao pivô de rotação em .
Passo 1
Temos o valor do momento de inércia da haste com relação ao eixo perpendicular passando pelo seu centro de massa:
Mas queremos o momento de inércia com relação ao eixo passando pelo pivô no qual a haste está presa.
Opa, isso está com cara de teorema dos eixos paralelos...
Conseguimos calcular o novo momento de inércia com:
Então, basta achar a distância entre os eixos que matamos a questão.
Passo 2
Aonde está o centro de massa da haste?
Como a haste é longa e fina, vamos considerar que a massa é uniformemente distribuida.
Assim, temos que o centro de massa se localiza no centro da haste. Ou seja, à uma distância da extremidade da barra:
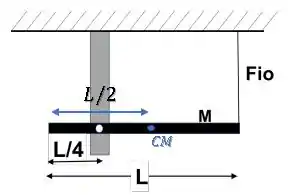
Logo, a distância entre os eixos que passam pelo centro de massa e pelo pivô será:
Passo 3
Agora, podemos substituir os valores no teorema e achamos o novo momento de inércia:
Resposta
(a)