1. Determine todas as raízes da equação bem como suas respectivas multiplicidades.
Passo 1
Fala meus chuchuzinhos da UFPE, bora matar essa questão de Cálculo 1?

Bom galera, nessa questão nós temos uma equação polinomial e ela nos pede para encontrar as raízes dessa equação.
Basicamente, o que queremos encontrar aqui é o valor de que de fato zera essa equação.
Como esse polinômio ele é do quinto grau, nós não temos como simplesmente usar bhaskara, pois bhaskara só serve para um polinômio de segundo grau.
Por conta disso, vamos precisar olhar para a cara do nosso polinômio e verificar alguns valores padrão para a raíz.
Também vamos precisar usar a divisão de polinômio, para ir reduzindo o grau do nosso polinômio e facilitar a nossa vida ao encontrar as raízes, então bora lá?
Passo 2
Bom, nosso polinômio é o seguinte:
E a pergunta que temos é: quais são os valores de que zeram esse polinômio, ou seja, quais as raízes dele.
A primeira raíz que podemos encontrar aqui é o .
Afinal, o nosso polinômio não tem nenhum termo independente, isso é, nenhum termo que não multiplique por , portanto, se , todo esse polinômio também vale zero:
Beleza, agora que descobrimos uma raíz, vamos reescrever esse polinômio para diminuir o grau dele.
A regra aqui é a seguinte, você vai dividir o polinômio por , que nesse caso , então dividindo o polinômio por , teremos:
Com isso, podemos reescrever nosso polinômio como sendo:
Agora temos uma multiplicação de polinômio e o termo possui raíz , agora vamos procurar pelas demais raízes que estão no termo
Passo 3
Bom, agora não temos muito o que fazer, vamos tentar chutar valores que zerem esse nosso termo, vou começar tentando o .
Opa, conseguimos zerar o nosso termo, portanto é uma raíz. Agora, para reduzir o grau desse termo, vamos dividir por que no caso é .
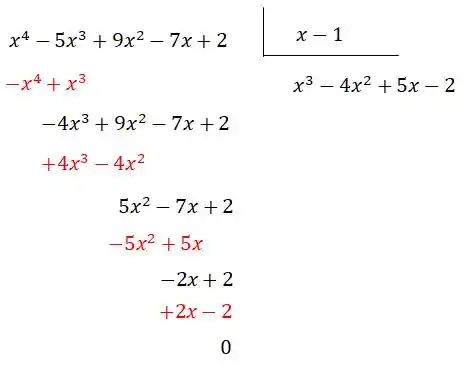
Com isso podemos reescrever o nosso polinômio da seguinte forma:
E sabemos que até o momento e são raízes do polinômio, ambas de multiplicidade um até o momento. Vamos agora procurar pelas raízes que estão no termo
Passo 4
Mesmo processo, chutar valores. Aqui você pode chutar de novo o valor , pois pode acontecer dessa raiz aparecer duas vezes, nada impede. Bom, vamos ver se é o caso:
Opa, zeramos o nosso polinômio, portanto é uma raíz. Vamos agora dividir o nosso termo por para diminuir o grau do nosso polinômio:
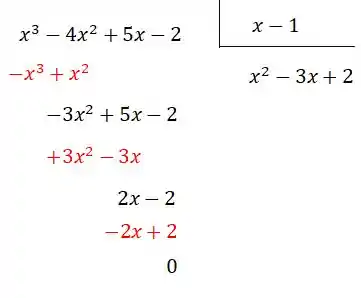
Portanto, podemos reescrever nosso polinômio como sendo:
E as raízes são com multiplicidade e com multiplicidade 2. Agora temos um termo de segundo grau e para encontrar as raízes dele podemos usar Bhaskara!!
Passo 5
Aplicando Bhaskara em , teremos:
Portanto encontramos aqui as raízes e , sendo que já era uma raíz de multiplicidade 2 e agora descobrimos que ela é de multiplicidade 3. Dessa forma, podemos reescrever nosso polinômio como:
E as raízes são: