Quais das opções abaixo são raízes da equação
- 1,2,-1
- -1,-2,1
- 1,-2,1
- -1,-2,-1
Passo 1
Fala aííí!! Vamos encontrar as raízes dessa equação do terceiro grau?? Se você reparar, não temos o em todos os termos da equação, então não podemos usar aquele método de colocar em evidência o em comum a todos os termos...

Então como podemos atacar esse exercício?? Utilizaremos o processo de Briot-Ruffini! Com ele conseguiremos reduzir o grau do nosso polinômio até chegar numa equação que conseguimos resolver!!
Para usá-lo, precisamos conhecer pelo menos uma raiz da expressão que queremos reduzir o grau. Nesse caso, vamos testar alguns valores de e ver se damos sorte:
Vamos primeiro testar
Substituindo o valor, temos
Opa, essa igualdade não é verdade! . Logo, não é raíz dessa equação!
Vamos testar
Substituindo o valor, temos
Opaaaaa, com , nossa expressão zerou, o que significa que a igualdade será válida e é uma raiz da nossa equação.
Passo 2
Agora sim, vamos a Briot Ruffini, com esse método vamos reescrever nossa equação como uma multiplicação de , onde esse é a raiz que conhecemos, vezes um outro polinômio de grau menor. No nosso caso, teremos:
Beleza?! Então vamos lá! Primeira coisa que faremos é armar o quadro:

Na parte superior esquerda, colocamos a raiz que já conhecemos, no caso, :

Na parte superior direita, colocamos os coeficientes da expressão que queremos reduzir:
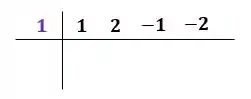
Agora, vamos repetir o primeiro coeficiente da parte superior direita na parte de baixo:
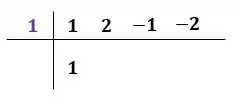
E multiplicar o número que desceu pela raiz conhecida:
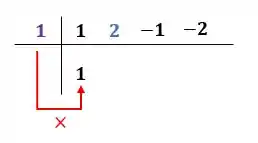
![]()
Agora, some o resultado com o segundo coeficiente à direita
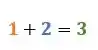
e coloque o resultado logo abaixo deste:

Beleza?!

Agora vamos repetir o processo até chegar no último coeficiente:
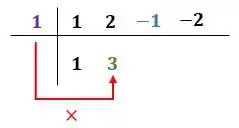
![]()
Agora o resultado da multiplicação somamos com o terceiro coeficiente à direita
![]()
E colocaremos o resultado logo abaixo deste:
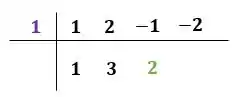
Mais uma vez, pra encerrar:
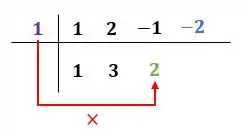
Fazendo a multiplicação, temos
![]()
O resultado multiplicaremos com somamos com o quarto coeficiente à direita
![]()
E colocaremos o resultado logo abaixo deste:
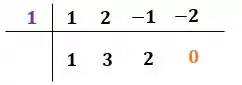
O último termo do resultado é o resto, mas como o resto é zero, não precisamos nos preocupar com ele. Fica tranquilo que a ideia aqui é sempre encontrarmos zero mesmo, então vamos seguir!

Agora, vamos escrever os três números restantes que encontramos como coeficientes de uma expressão do 2º grau:
Essa expressão é o polinômio que estávamos procurando e podemos reescrever nossa equação como:
Portanto, nossas soluções serão:
O resultado da primeira parte, já conhecemos:
Para a segunda, como temos uma equação do 2º grau, vamos usar a fórmula de Bhaskara:
Beleza?!

Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Passo 3
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Então, as soluções para nossa equação são
Logo, a resposta é a letra (B)