Exercícios Resolvidos de Produto Vetorial

Exercício 14 1 2 3 4 5 6 7 8 9 10 11 12 13 15

Enunciado

Calcule o produto vetorial e entre os vetores mostrados nas figuras.

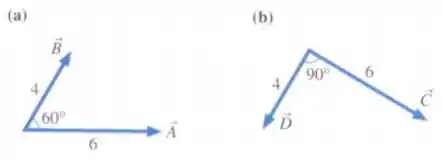
Passo 1

Beleza, primeiro vamos fazer o produto vetorial para e .

Todo produto vetorial me retorna um vetor. Vou chamar esse vetor, nesse caso, de .

Para calcular o módulo de , usaremos:

Agora precisamos nos preocupar com a direção e sentido de . E é agora que usaremos a regra da mão direita.

Então faz comigo: Coloque seus quatro dedos da mão direita com exceção do dedão na direção de . Agora, coloque sua palma da mão na direção de . Agora, fecha sua mão e você vai ver que seu polegar está apontando para fora da página (ou tela, já que vc deve estar lendo isso em um PC, notebook, ou no nosso app pelo celular).

Logo, podemos dizer que P tem módulo 20,8 e aponta para fora da tela.

Vamos dizer que o vetor unitário que dá a direção para fora da tela é o .

Passo 2

É o mesmo esquema do Passo 1, só que para .

Primeiro encontramos o módulo de .

E utilizando a regra da mão direita, veremos que o nosso polegar aponta para dentro da página/tela, e portanto também aponta nessa direção.

Utilizando a notação onde é o vetor unitário que aponta para fora da tela, teremos:

Resposta

(a)

(b)

Exercícios de Livros Relacionados

O vetor d 1 → , é paralelo ao semieixo y negativo e o vetor d 2 → é paralelo ao semieixo x positivo. Determine a orientação (a) de d 2 → 4 e (b) de - d 1 → 4 Determine o módulo (c) de d 1 → ⋅ d 2

Os vetores a → e b → estão no plano x y . a → tem módulo 8,00 e ângulo 130 ° ; b → tem componentes b x = - 7,72 e b y = - 9,20 . Determine o ângulo entre o semieixo y negativo e (a) o vetor a → ,

Por meio de desenhos simples dos produtos vetoriais apropriados, demonstre que b) | A → × B → | pode ser interpretado como o produto do módulo de A → vezes o componente de B → perpendicular a A → , ou

Dois vetores, r →es → , estão no plano x y . Os módulos dos vetores são 4,50 unidades e 7,30 unidades, respectivamente, e eles estão orientados a 320 °e85,0 ° , respectivamente, no sentido anti-horári

Se d vec 1 = 3 vec i - 2 vec j + 4 vec k e d vec 2 = - 5 vec i + 2 vec j – vec k , determine (vec d_1 + vec d_2) . (vec d_1 xx 4 vec d_2) .