Para os vetores e indicados na figura abaixo:
- Ache o módulo e a direção do produto vetorial
- Ache o módulo e a direção do produto vetorial
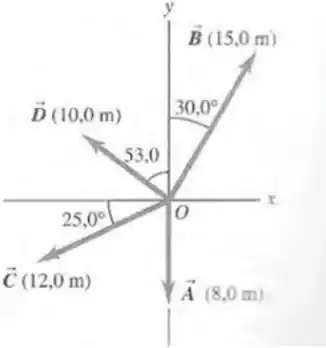
Dados:
Passo 1
Para calcularmos o módulo do produto vetorial vamos usar a seguinte fórmula:
É importante lembrar que o produto vetorial entre vetores não é comutativo, porém, pode ser considerado anti-comutativo?
Que???
Passo 2
Alternativa a)
Calculando o módulo de vetor:
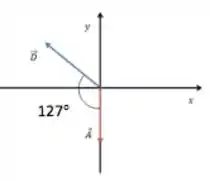
Substituindo os valores na equação do módulo do vetor temos:
Passo 3
Alternativa b)
Calculando o módulo de vetor:
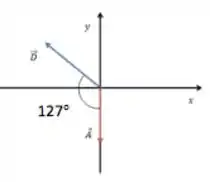
Substituindo os valores na equação do módulo do vetor temos:
Passo 4
Mas e a direção? Você não falou nada cara! Você deu a mesma resposta nas duas alternativas.
A direção dos vetores é a mesma. Os dois vetores passam pelo centro do eixo , perpendicular ao plano, pois os vetores precisam ser perpendiculares tanto à quanto à , na direção de .
Mas qual a diferença então?
A diferença é o sentido que os vetores possuem. Um vetor tem o sentido oposto ao outro.
Se você fizer a regra da mão direita , vai ver que o produto escalar de estará em e o será no sentido , que vai estar “furando” a tela do seu PC. :P
Resposta
Alternativa a),
Alternativa b)