A figura abaixo mostra um paralelogramo cujos lados são os vetores e
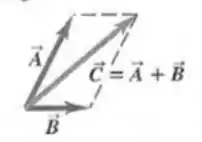
- Mostre que o módulo do produto vetorial destes vetores é igual à área do paralelogramo . (Sugestão: )
- Qual é o ângulo entre o produto vetorial e o plano deste paralelogramo?
Passo 1
Sabemos que a fórmula do módulo de um produto vetorial é:
O que temos que fazer é provar que a área do paralelogramo tem essa mesma fórmula
Passo 2
Alternativa a)
O paralelogramo formado pelos vetores tem a seguinte forma:
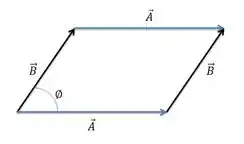
Como o problema deu uma dica, vamos usar, né?
Para calcular a área desse paralelogramo vamos dividir ele em dois triângulos, pois assim podemos usar a fórmula da área que ele deu.
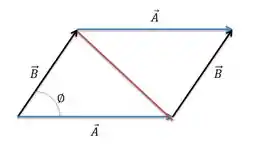
Passo 3
Como podemos perceber, divimos á area do paralelogramo em dois triângulos iguais, ou seja, se acharmos a área do triângulo conseguimos achar a área do paraleogramo.
Para calcular a área do triângulo precisamos achar a altura relativa a base.
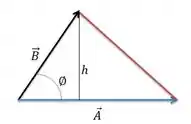
Considerando a altura relativa à base, temos que:
Passo 4
Como a fórmula da área de um triângulo é:
Substituindo os valores temos:
Escrevendo em função de :
Como já sabemos á relação da área do triângulo e do paralelogramo temos que:
Passo 5
Alternativa b)
Como os vetores formam um plano, que no caso é o plano do paralelogramo, e sabendo que o produto vetorial tem como resultado um vetor perpendicular à ambos, o vetor também é perpendicular ao plano formado pelos vetores: