Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Produto Vetorial

Ver Teoria
Exercício 111234567891012131415

Enunciado

UFABC – Fenômenos Mecânicos – Lista 6 – Questão 04.a

Dados dois vetores quaisquer a → = a x i ^ + a y j ^ + a z k ^ e b → = b x i ^ + b y j ^ + b z k ^ , dependentes do tempo,

  1. Mostre explicitamente que

d d t a → × b → = d a → d t × b → + a → × d b → d t

Passo 1

Olá pessoal, tudo bem? Vamos praticar o cálculo vetorial? Essa questão é complicada, mas vou te ajudar! O problema nos deu dois vetores a → e b → , e pediu para mostrarmos explicitamente essa propriedade aqui:

d d t a → × b → = d a → d t × b → + a → × d b → d t

Mas como fazer isso?

Calculando o que se pede de cada lado individualmente e depois comparar os resultados!

Assim:

  • Vamos começar pelo lado esquerdo da igualdade, calculando o produto vetorial entre os vetores e depois derivando em relação ao tempo (para fazer derivada de vetor basta derivar componente a componente)
  • Depois vamos para o lado direito: fazer aqueles dois produtos vetoriais separadamente e depois somar os resultados
  • Por fim, comparar os resultados e torcer para que dê tudo certo!

Mas relaxa, vou fazer passo a passo com você! Vamos lá?

Passo 2

Vamos começar calculando o produto vetorial entre

a → = a x i ^ + a y j ^ + a z k ^

b → = b x i ^ + b y j ^ + b z k ^

Basta resolver o determinante de terceira ordem! Aqui atenção: fica de olho na ordem dos vetores! Isso faz diferença no resultado!

Vamos calcular o produto vetorial entre dois vetores a → e b → :

a → × b → = i ^ j ^ k ^ a x a y a z b x b y b z

E daqui em diante é como resolver um determinante de terceira ordem

a → × b → = a y b z - a z b y i ^ + a z b x - a x b z j ^ + a x b y - a y b x k ^

Beleza? Agora vamos derivar em relação ao tempo cada componente! Todas as componentes variam com o tempo, então para cada produto de a e b , precisamos aplicar a regra do produto para derivar!

Primeiro para a componente i ^ :

d d t a → × b → x = d d t a y b z - a z b y = b z d a y d t + a y d b z d t - a z d b y d t - b y d a z d t

Beleza? Tranquilo até aqui?

j ^ e k ^ do vetor:

d d t a → × b → y = d d t a z b x - a x b z = a z d b x d t + b x d a z d t - a x d b z d t - b z d a x d t

Certo?

E por fim a última componente:

d d t a → × b → z = d d t a x b y - a y b x = a x d b y d t + b y d a x d t - a y d b x d t - b x d a y d t

E é isso! O vetor d d t a → × b → tem essas três componentes:

d d t a → × b → x = b z d a y d t + a y d b z d t - a z d b y d t - b y d a z d t d d t a → × b → y = a z d b x d t + b x d a z d t - a x d b z d t - b z d a x d t d d t a → × b → z = a x d b y d t + b y d a x d t - a y d b x d t - b x d a y d t

Tira um print desse resultado! Vamos agora passar para o cálculo do lado direito da igualdade para depois comparar os resultados!

Passo 3

Agora o lado direito da igualdade:

d a → d t × b → ⏝ 1 º   + a → × d b → d t ⏝ 2 º

Vamos começar calculando o produto vetorial entre d a → d t e b → !

Partindo do produto vetorial normal (nosso de cada dia)

d a → d t × b → = i ^ j ^ k ^ d a x d t d a y d t d a z d t b x b y b z =

= d a y d t b z - d a z d t b y i ^ + d a z d t b x - d a x d t b z j ^ + d a x d t b y - d a y d t b x k ^

Notou que o resultado já é bem parecido com o que encontramos como resultado do lado esquerdo? Lá no final do passo 2? Pois é! Agora falta calcular o segundo pedaço da igualdade e somar os resultados!

O segundo pedaço:

a → × d b → d t ⏝ 2 º

Agora vamos calcular esse produto vetorial:

a → × d b → d t = i ^ j ^ k ^ a x a y a z d b x d t d b y d t d b z d t =

= a y d b z d t     - a z d b y d t i ^ + a z d b x d t - a x d b z d t j ^ + a x d b y d t - a y d b x d t k ^

Beleza?

Agora vamos somar esses dois resultados! Para somar vetores, basta somar componente a componente:

d a → d t × b → + a → × d b → d t = d a y d t b z - d a z d t b y i ^ + d a z d t b x - d a x d t b z j ^ + d a x d t b y - d a y d t b x k ^ + a y d b z d t     - a z d b y d t i ^ + a z d b x d t - a x d b z d t j ^ + a x d b y d t - a y d b x d t k ^

Para facilitar, vou somar componente a componente separadamente:

d a → d t × b → + a → × d b → d t x = b z d a y d t + a y d b z d t - b y d a z d t - a z d b y d t

Agora a componente j ^ :

d a → d t × b → + a → × d b → d t y = b x d a z d t + a z d b x d t - b z d a x d t - a x d b z d t

Por fim a k ^ :

d a → d t × b → + a → × d b → d t z = b y d a x d t + a x d b y d t - b x d a y d t - a y d b x d t

Beleza?

Passo 4

Agora chegou a parte boa! Comparar os resultados!! Vamos resgatar o resultado do passo 2 (falei para tirar print):

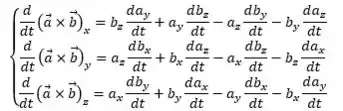
E agora vamos comparar com o resultado do passo 3:

viu, igual! Sendo assim mostramos que:

d d t a → × b → = d a → d t × b → + a → × d b → d t

Como o problema pediu!

Como eu me sinto depois de uma questão assim:

Espero ter ajudado!

Resposta

d e m o n s t r a ç ã o

Exercícios de Livros Relacionados

O vetor d 1 → , é paralelo ao semieixo y   negativo e o vetor d 2 → é paralelo ao semieixo x   positivo. Determine a orientação (a) de d 2 → 4 e (b) de - d 1 → 4 Determine o módulo (c) de d 1 → ⋅ d 2
Os vetores a → e b → estão no plano x y . a → tem módulo 8,00 e ângulo 130 ° ; b → tem componentes b x   =   - 7,72 e b y = - 9,20 . Determine o ângulo entre o semieixo y negativo e (a) o vetor a → ,
Por meio de desenhos simples dos produtos vetoriais apropriados, demonstre que b) | A → × B → | pode ser interpretado como o produto do módulo de A → vezes o componente de B → perpendicular a A → , ou
Dois vetores, r →es → , estão no plano x y . Os módulos dos vetores são 4,50 unidades e 7,30 unidades, respectivamente, e eles estão orientados a 320 °e85,0 ° , respectivamente, no sentido anti-horári
Se d vec 1 = 3 vec i - 2 vec j + 4 vec k e d vec 2 = - 5 vec i + 2 vec j – vec k , determine (vec d_1 + vec d_2) . (vec d_1 xx 4 vec d_2) .