UFSCAR – Cálculo 1 – P1 – Questão 1c
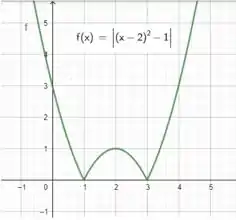
Considere a função abaixo
- Esboce o gráfico de . (Complete quadrados e use deslocamento e reflexões)
Passo 1
Fala pessoal, tudo beleza?
Essa questão é uma continuação, então se você ficar com alguma dúvida do que veio antes, é só consultar!
Nossa função é essa aqui
E nesse último item o problema pede para esboçarmos o gráfico de !
E temos algumas orientações: precisamos completar quadrados e usar a técnica de deslocamento e reflexão para isso! Então vamos lá!
Passo 2
Nossa função é essa aqui
Dentro do módulo temos uma função quadrática então quando você se deparar com ela precisa lembrar imediatamente de: completar quadrados!
Aí lembrando que temos
Aí nossa função modular fica assim
Tudo bem até aqui?
Passo 3
Agora nossa missão é entender os deslocamentos feitos!
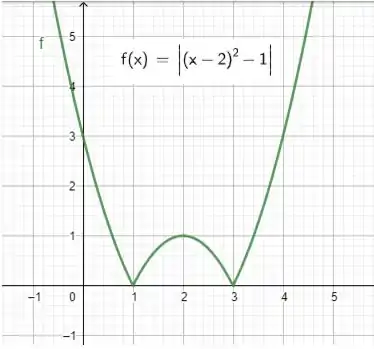
Primeiro vamos olhar nossa função final
E identificar todas as mudanças que foram feitas! Começando olhando o , ele era um que foi deslocado para a direita duas unidades, ficando
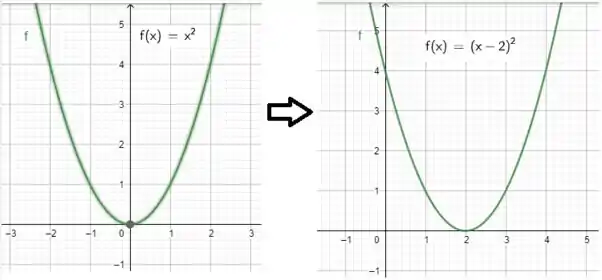O gráfico até agora está assim
Depois de deslocarmos para a direita o , o que foi feito? Subtraímos 1 unidade! Olha nossa função
Deslocando em estaremos ‘descendo um degrau’, e todo gráfico fica um degrau a menos na imagem.
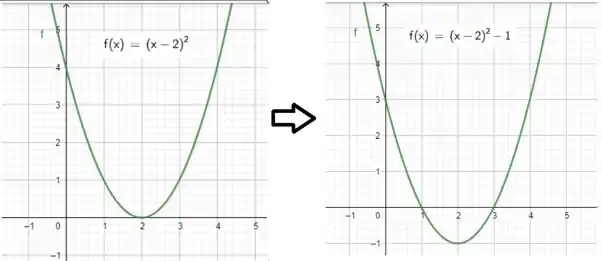
Mas notem a expressão da função que temos! Está quase igual à !
O que falta? O módulo!
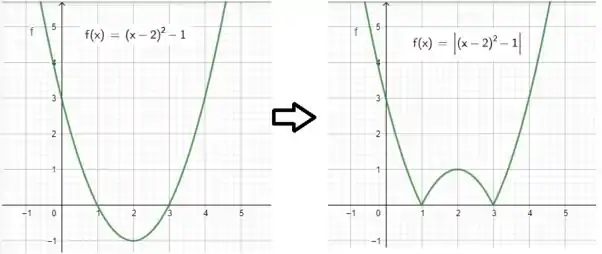
Pronto! Temos nosso gráfico! O esboço da é
Espero ter ajudado! Até a próxima!
Resposta
