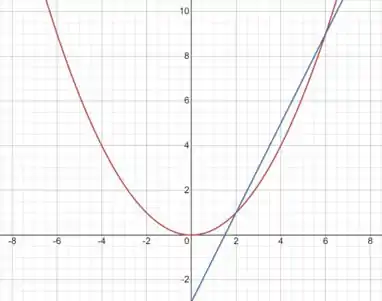
C4) Considere a função .
b) Marque os pontos do gráfico de de abscissas e e desenhe a reta que passa por esses pontos.
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

O enunciado nos informa duas coordenadas abscissas. Mas o que isso significa?
Coordenadas no eixo das abscissas nada mais são do que coordenadas do eixo . Portanto, para definirmos dois pontos, precisamos aplicar essas coordenadas na função e encontrar as coordenadas de . Então:
Para :
Encontramos o ponto A .
Para :
Encontramos o ponto B .
Passo 2
Agora que conhecemos os dois pontos, podemos ligá-los:
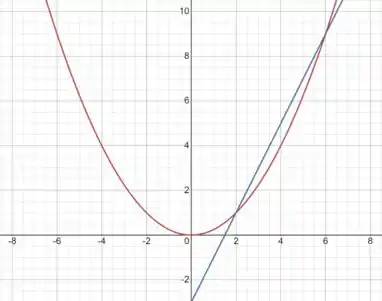
Ufa! Terminamos!

Pra essa questão é isso pessoal! Bora pra mais uma?
Resposta