Os dois vetores e são desenhados a partir de um mesmo ponto e
- Mostre que quando , o ângulo entre os vetores e é .
- Mostre que quando , o ângulo entre os vetores e é maior do que .
- Mostre que quando , o ângulo entre os vetores e está compreendido entre e .
Considere somente ângulos entre e .
Passo 1
Nessa questão estamos trabalhando com soma de vetores e o ângulo entre eles. Tudo tranquilo até aqui? Se liga nesse desenho aqui que ele vai ajudar a gente a entender o método de soma de veteores que será usado.
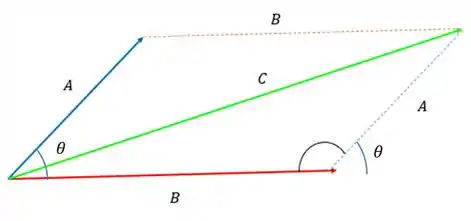
Se lembra que tínhamos dois tipos de soma? A pelo método do paralelogramo e o método geométrico? Aqui vamos usar o método do paralelogramo, pois ele falou que eles partem do mesmo ponto.
E no enunciado foi dado o ângulo entre os vetores , que como podemos ver no desenho acima é o mesmo ângulo externo do paralelogramo que é o ângulo usado na fórmula!
Passo 2
Analisando a equação percebemos que o que está mudando de uma letra pra outra é o ângulo Por isso, vamos analisar o . Pelo círculo trigonométrico sabemos que o cosseno nesse intervalo varia de 1 até -1.
Passo 3
Letra a) Quando temos , temo s o seguinte:
Logo:
Mas como o ângulo precisa estar entre e , teremos:
Passo 4
Letra b)
Quando temos , achamos que:
Se o cosseno do ângulo varia de até 1 mas nesse caso deve ser menor que 0 temos os seguintes limites pro cosseno.
Pelo intervalo analisado só podemos ter valores negativos de cosseno menores que 0. Essa variação de cosseno pode ser visualizada melhor usando o circulo trigonométrico.
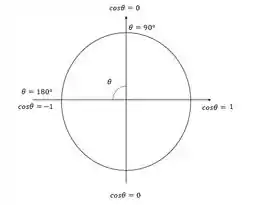
Através do círculo podemos ver que o cosseno tem valor quando for e vale quando for , e dentro desse intervalo é negativo.
Logo, provamos que
Passo 5
Letra c)
Quando temos , achamos que:
Analisando novamente o círculo podemos ver que o cosseno é positivo no intervalo dado:
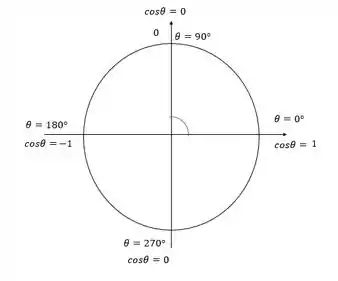
Aonde vemos o cosseno do ângulo vale para e para , sendo positivo nesse intervalo:
Resposta
Ei, a resposta está no passo a passo :)