Você deve programar um braço robótico em uma linha de montagem para mover no plano . Seu primeiro deslocamento é ; seu segundo deslocamento é de magnitude e direção medido no sentido do eixo para o eixo . O vetor resultante dos dois deslocamentos também deve ter uma magnitude de , mas uma direção medida no sentido do eixo da direção do eixo .
(a) Desenhe o diagrama de soma vetorial para esses vetores, com a escala aproximada.
(b) Encontre os componentes de .
(c) Encontre a magnitude e a direção de .
Passo 1
Oii gente linda, tudo bem com vocês?? Bora pra mais uma?
Bom o enunciado nos descreve como o braço robótico se desloca ao longo do plano . Já na letra (a) nos é solicitado o esboço desses vetores no plano. Então vamos ter que posicionar esses vetores de modo que o vetor represente a soma vetorial dos vetores e . A princípio vamos posicionar os vetores e como o enunciado descreve, em seguida, vamos utilizar a regra do paralelogramo para estimar a direção e o sentido do vetor .
Logo,
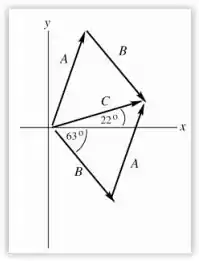
Passo 2
Já na letra (b) temos que encontrar as componentes do vetor . E como poderemos fazer isso???
Vamos começar escrevendo a soma vetorial que o enunciado nos forneceu em relação a cada um dos eixos. Começando pelo eixo :
Belezinha, temos até então a magnitude e a direção dos vetores e , entretanto, ainda não temos suas respectivas projeções para o eixo . Para encontrarmos essas projeções vamos ter que lembrar de algumas funções trigonométricas.
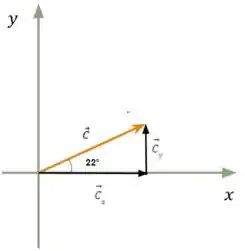
Como o vetor e suas componentes se rearranjam formando um triângulo retângulo assim como ilustrado na imagem acima concluímos que as projeções de podem ser dadas por:
e
Após realizar o mesmo procedimento para o vetor reescrevemos a nossa soma vetorial da seguinte forma:
Substituindo agora com os valores correspondentes,
Passo 3
Agora vamos seguir os mesmos procedimentos do passo anterior para projetar as componentes em relação ao eixo :
Passo 4
Já temos as componentes de e como já vimos no passo 1, que o vetor sempre forma um triângulo retângulo com suas componentes. Logo, para encontrarmos a magnitude do vetor em questão basta aplicarmos o Teorema de Pitágoras da seguinte forma:
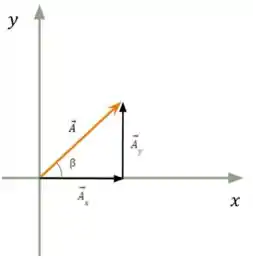
E por fim para conseguirmos encontrar a direção em que se encontra este vetor vamos ter que descobrir qual é o ângulo que esse vetor faz com o eixo . O legal aqui é que essa ideia de localizar a direção a partir de ângulos, é a base do sistema de localização de aeronaves, submarinos, entre outros.
Observando a imagem acima temos que :
Tá, e agora??? Como poderemos chegar no valor do ângulo em questão a partir da sua tangente???

Vamos utilizar a função inversa da função tangente, ou seja, a função arco-tangente:
Prontos agora achamos o nosso ângulo! Perfeito :)
Então nessa questão aprendemos a esboçar vetores, vimos também como encontrar um vetor a partir de uma soma vetorial e já no finalzinhoooo utilizamos alguns artifícios fundamentais para encontrar a magnitude e a direção de um vetor inicialmente desconhecido. Showw?!!
Bons Estudos!
Resposta
a)
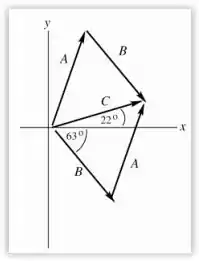
b)
e
c)
Magnitude :
Direção: em relação ao eixo